题目内容
已知函数f(x)=2sinx•cos(x-
)+asin(2x+
)(a为常数)的图象经过点(
,
)
(Ⅰ)求a的值及函数f(x)的最小正周期;
(Ⅱ)解不等式f(x)≥0.
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 3 |
(Ⅰ)求a的值及函数f(x)的最小正周期;
(Ⅱ)解不等式f(x)≥0.
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由已知可得2sin
cos(-
)+asin
=
,从而解得a=1,由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin2x+
,由周期公式即可求最小正周期T.
(2)由f(x)≥0,知:sin2x≥-
,由正弦函数的图象解得2kπ-
≤2x≤2kπ+
(k∈Z),即可得f(x)≥0的解集.
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 3 |
| ||
| 2 |
(2)由f(x)≥0,知:sin2x≥-
| ||
| 2 |
| π |
| 3 |
| 4π |
| 3 |
解答:
解:(1)函数f(x)=2sinx•cos(x-
)+asin(2x+
)(a为常数)的图象经过点(
,
),
则有:2sin
cos(-
)+asin
=
,
故解得:a=1,
∴f(x)=2sinx•cos(x-
)+sin(2x+
),
=2sinx(cosxcos
+sinxsin
)+sin2xcos
+cos2xsin
,
=2sin2xcos
+(2sin2x+cos2x)sin
,
=sin2x+sin
,
=sin2x+
,
∴最小正周期T=
=π…6分
(2)由f(x)≥0,知:sin2x≥-
,
∴2kπ-
≤2x≤2kπ+
(k∈Z),
∴f(x)≥0的解集为:[kπ-
,kπ+
](k∈Z)…12分
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 3 |
则有:2sin
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 3 |
故解得:a=1,
∴f(x)=2sinx•cos(x-
| π |
| 3 |
| π |
| 3 |
=2sinx(cosxcos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=2sin2xcos
| π |
| 3 |
| π |
| 3 |
=sin2x+sin
| π |
| 3 |
=sin2x+
| ||
| 2 |
∴最小正周期T=
| 2π |
| 2 |
(2)由f(x)≥0,知:sin2x≥-
| ||
| 2 |
∴2kπ-
| π |
| 3 |
| 4π |
| 3 |
∴f(x)≥0的解集为:[kπ-
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
若α表示平面,a,b表示直线,给定下列四个说法:其中正确说法的序号是( )
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
| A、①和② | B、②和④ |
| C、③和④ | D、①和③ |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )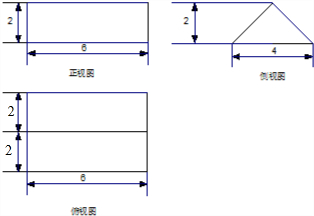

| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |