题目内容
已知正项等比数列{an}中,a1+a2=6,a3+a4=24.
(Ⅰ)求数列{an}的通项;
(Ⅱ)数列{bn}满足bn=log2an,求数列{an+bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项;
(Ⅱ)数列{bn}满足bn=log2an,求数列{an+bn}的前n项和Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等比数列通项公式列出方程组,求出首项和公比,由此能求出{an}的通项公式.
(Ⅱ)由bn=log2an=log22n=n,得an+bn=2n+n,由此利用分组求和法能求出数列{an+bn}的前n项和.
(Ⅱ)由bn=log2an=log22n=n,得an+bn=2n+n,由此利用分组求和法能求出数列{an+bn}的前n项和.
解答:
(本小题满分13分)
解:(Ⅰ)∵正项等比数列{an}中,a1+a2=6,a3+a4=24,
∴
,且q>0,
解得a1=2,q=2,
∴an=a1•qn-1=2•2n-1=2n.
(Ⅱ)∵bn=log2an=log22n=n,
∴an+bn=2n+n
∴数列{an+bn}的前n项和:
Tn=(2+22+23+…+2n)+(1+2+3+…+n)
=
+
=2n+1-2+
+
.
解:(Ⅰ)∵正项等比数列{an}中,a1+a2=6,a3+a4=24,
∴
|
解得a1=2,q=2,
∴an=a1•qn-1=2•2n-1=2n.
(Ⅱ)∵bn=log2an=log22n=n,
∴an+bn=2n+n
∴数列{an+bn}的前n项和:
Tn=(2+22+23+…+2n)+(1+2+3+…+n)
=
| 2(2n-1) |
| 2-1 |
| n(n+1) |
| 2 |
=2n+1-2+
| n2 |
| 2 |
| n |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )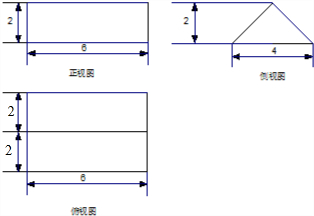

| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |
在如图所示的程序框图中,若f0(x)=xex,则输出的结果是( )
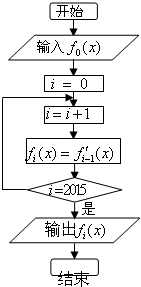

| A、2016ex+xex |
| B、2015ex+xex |
| C、2014ex+xex |
| D、2013ex+x |
已知圆M过定点(2,0)且圆心M在抛物线y2=4x上运动,若y轴截圆M所得的弦长为AB,则弦长|AB|等于( )
| A、4 | B、3 |
| C、2 | D、与点M位置有关的值 |
