题目内容
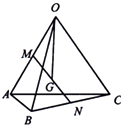 已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设
已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设| OG |
| OA |
| OB |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用已知条件,转化向量关系,通过平面向量的运算,推出结果即可.
解答:
解:空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,
可知
=
,
=
(
+
),
=
(
+
).
∴
=
(
+
(
+
))=
=
+
+
,
∵
=x
+y
+z
,∴x,y,z的值分别是
,
,
.
故选:A.
可知
| OM |
| 1 |
| 2 |
| OA |
| ON |
| 1 |
| 2 |
| OB |
| OC |
| OG |
| 1 |
| 2 |
| OM |
| ON |
∴
| OG |
| 1 |
| 2 |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| OC |
| OG |
| 1 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
| 1 |
| 4 |
| OC |
∵
| OG |
| OA |
| OB |
| OC |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故选:A.
点评:本题考查平面向量基本定理的应用,空间向量转化为平面向量的解题的关键.

练习册系列答案
相关题目
在区间[0,π]上随机取一个实数x,使得sinx∈[0,
]的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若α表示平面,a,b表示直线,给定下列四个说法:其中正确说法的序号是( )
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
| A、①和② | B、②和④ |
| C、③和④ | D、①和③ |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )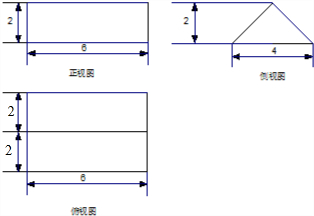

| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |
