题目内容
5.方程ex=5-x的根所在的大致区间为( )| A. | ($\frac{1}{2}$,1) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,2) | D. | (2,$\frac{5}{2}$) |
分析 方程ex=5-x的解转化为函数f(x)=ex+x-5的零点问题,把区间端点函数值代入验证即可.
解答 解;由ex=5-x得ex+x-5=0,
设f(x)=ex+x-5,则函数f(x)单调递增,
∴f(0)=e+1-5<0
f($\frac{3}{2}$)=${e}^{\frac{3}{2}}$+$\frac{3}{2}$-5>$(\frac{5}{2})^{\frac{3}{2}}$-$\frac{7}{2}$=$\sqrt{\frac{125}{8}}$-$\sqrt{\frac{98}{8}}$>0
∴f(x)=ex+x-5在区间(1,$\frac{3}{2}$有一个零点,
即方程ex+x=5在区间(1,$\frac{3}{2}$)有解,
故选:B.
点评 考查方程的根和函数零点之间的关系,即函数零点的判定定理,体现了转化的思想方法,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知复数$z=\frac{{1+2{i^3}}}{2+i}$(i为虚数单位),则z在复平面内所对应点的坐标为( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
20.设i是虚数但单位,则复数$z=\frac{2i+3}{1-i}$的共轭复数的虚部为( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{2}$ |
14.已知随机变量ξ服从正态分布N(1,δ2),P(ξ≤-1)=0.012,则P(1<ξ<3)=( )
| A. | 0.488 | B. | 0.494 | C. | 0.502 | D. | 0.512 |
15.在长为10cm的线段AB上任取一点C,现作一矩形,邻边长分别等于AC,CB的长,则该矩形面积不小于9cm2的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
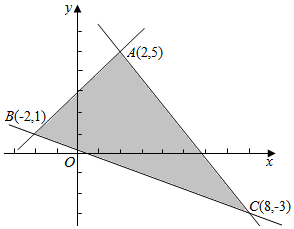 直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:
直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示: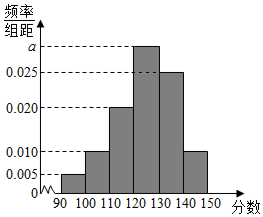 某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.