题目内容
向量
=(-3,4),
=-2
,若A点的坐标是(1,2),则B点的坐标为( )
| a |
| AB |
| a |
| A、(-7,8) |
| B、(7,-6) |
| C、(-5,10) |
| D、(9,-4) |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:设出B的坐标,利用向量关系求出B的坐标即可.
解答:
解:向量
=(-3,4),
=-2
,
∴
=-2
=(6,-8),
A点的坐标是(1,2),则B点的坐标设为(x,y),
∴(6,-8)=(x-1,y-2),
∴x=7,y=-6,
∴B(7,-6).
故选:B.
| a |
| AB |
| a |
∴
| AB |
| a |
A点的坐标是(1,2),则B点的坐标设为(x,y),
∴(6,-8)=(x-1,y-2),
∴x=7,y=-6,
∴B(7,-6).
故选:B.
点评:本题给出一个向量的坐标,着重考查了平面向量的坐标运算和向量模的公式等知识,属于基础题.

练习册系列答案
相关题目
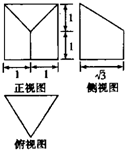
如图为一个几何体是三视图,则该几何体的表面积(不考虑接触点)为( )

A、6+
| ||
| B、32+π | ||
C、18+
| ||
D、18+2
|
已知函数f(x)的定义域为R,对于定义域内的任意x,满足f(x)=-f(x+1),且当-1<x≤1时,f(x)=1-x2,若函数g(x)=f(x)+x-a恰有两个零点,则实数a的所有可能取值构成的集合为( )
A、{a|a=2k+
| ||||
B、{a|a=2k-
| ||||
C、{a|a=2k+1或2k+
| ||||
| D、{a|a=2k+1,k∈Z} |
已知集合A={-1,2,3},B={y|y=x3,x∈A},则A∩B=( )
| A、{0} | B、{1} |
| C、{-1} | D、{0,1} |
设函数f(x)的定义域为D,若存在非零实数t使得对于任意x∈M(M⊆D),有x+t∈D,且f(x+t)≥f(x),则称f(x)为M上的“t高调函数”.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的“4高调函数”,那么实数a的取值范围是( )
A、[-
| ||||||||
| B、[-1,1] | ||||||||
C、[-1,
| ||||||||
D、[-
|
在区间[0,π]内任取一个数x,则使sinx-cosx≤0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设复数z1=1+i,z2=
-i,其中i为虚数单位,则
的实部为( )
| 3 |
| z1 |
| z2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|