题目内容
已知集合A={-1，2，3}，B={y|y=x3，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{-1} | D、{0，1} |
考点：交集及其运算
专题：集合
分析：将A中元素代入y=x3，求出y的值，确定出B，找出两集合的交集即可．
解答：
解：将x=-1，2，3分别代入y=x3，得：y=-1，8，27，即B={-1，8，27}，
∵A={-1，2，3}，
∴A∩B={-1}．
故选：C．
∵A={-1，2，3}，
∴A∩B={-1}．
故选：C．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知a∈R，若
为实数，则a=（ ）
| 1+ai |
| 2-i |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
执行如图所示的程序框图，若输出b的值为15，则图中判断框内①处应填的数是（ ）| A、2 | B、3 | C、4 | D、5 |
向量
=（-3，4），
=-2
，若A点的坐标是（1，2），则B点的坐标为（ ）
| a |
| AB |
| a |
| A、（-7，8） |
| B、（7，-6） |
| C、（-5，10） |
| D、（9，-4） |
已知甲盒中仅有1个球且为红球，乙盒中有m个红球和n个蓝球（m≥3，n≥3），从乙盒中随机抽取i（i=1，2）个球放入甲盒中．
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
| A、p1＞p2，E（ξ1）＜E（ξ2） |
| B、p1＜p2，E（ξ1）＞E（ξ2） |
| C、p1＞p2，E（ξ1）＞E（ξ2） |
| D、p1＜p2，E（ξ1）＜E（ξ2） |
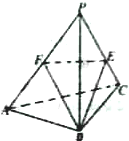如图：已知正三棱锥P-ABC，侧棱PA，PB，PC的长为2，且∠APB=30°，E，F分别是侧棱PC，PA上的动点，则△BEF的周长的最小值为（ ）A、8-4
| ||
| B、2 | ||
C、2
| ||
D、1+2
|
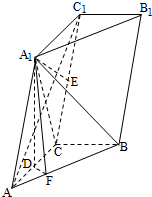如图，三棱柱ABC-A1B1C1中，点A1在平面ABC内的射影D在AC上，∠ACB=90°，BC=1，AC=CC1=2．