题目内容
现有A,B两个投资项目,投资两项目所获得利润分别是P和Q(万元),它们与投入资金x(万元)的关系依次是:其中P与x平方根成正比,且当x为4(万元)时P为1(万元),又Q与x成正比,当x为4(万元)时Q也是1(万元);某人甲有3万元资金投资.
(Ⅰ)分别求出P,Q与x的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
(Ⅰ)分别求出P,Q与x的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:(I)设P,Q与x的比例系数分别是k1,k2,则P=k1
,Q=k2x,根据当x为4(万元)时,P、Q为1(万元),可求出P,Q与x的函数关系式;
(Ⅱ)甲投资到A,B两项目的资金分别为x(万元),(3-x)(万元)(0≤x≤3),获得利润为y万元,根据(I)可得利润函数,利用配方法可求最大利润.
| x |
(Ⅱ)甲投资到A,B两项目的资金分别为x(万元),(3-x)(万元)(0≤x≤3),获得利润为y万元,根据(I)可得利润函数,利用配方法可求最大利润.
解答:
解:(I)设P,Q与x的比例系数分别是k1,k2,则P=k1
,Q=k2x且都过(4,1)…(1分)
所以:P=
(x≥0)…(2分),Q=
(x≥0)…(2分)
(Ⅱ)设甲投资到A,B两项目的资金分别为x(万元),(3-x)(万元)(0≤x≤3),获得利润为y万元…(1分)
由题意知:y=
+
=-
(
-1)2+1…(1分)
所以当
=1,即x=1时,ymax=1…(2分)
答:甲在A,B两项上分别投入为1万元和2万元,此时利润最大,最大利润为1万元..(1分)
| x |
所以:P=
| ||
| 2 |
| x |
| 4 |
(Ⅱ)设甲投资到A,B两项目的资金分别为x(万元),(3-x)(万元)(0≤x≤3),获得利润为y万元…(1分)
由题意知:y=
| ||
| 2 |
| 3-x |
| 4 |
| 1 |
| 4 |
| x |
所以当
| x |
答:甲在A,B两项上分别投入为1万元和2万元,此时利润最大,最大利润为1万元..(1分)
点评:本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,正确确定函数解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是( )
A、t>
| ||
B、t<
| ||
C、t≥
| ||
D、0<t<
|
a,b,c分别是△ABC的内角A,B,C的对边,下面能得出△ABC为锐角三角形的条件是( )
A、sinA+cosA=
| ||||
| B、tanA+tanB+tanC>0 | ||||
| C、b=3,c=3,B=30° | ||||
D、
|
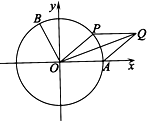 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且