题目内容
若函数f（x）=
，若f（a）＜0，则实数a的取值范围是 ．
|
考点：指、对数不等式的解法,其他不等式的解法
专题：计算题,不等式的解法及应用
分析：利用f（x）=
，依题意，分a＞0与a＜0讨论，利用对数函数的单调性质即可求得实数a的取值范围．
|
解答：
解：∵f（x）=
，
∴当a＞0时，f（a）＜0?log2a＜0，
解得：0＜a＜1；
当a＜0时，f（a）＜0?log
(-x)＜0=log
1，
∴-x＞1，
解得：x＜-1．
∴实数a的取值范围是：（-∞，-1）∪（0，1）．
故答案为：（-∞，-1）∪（0，1）．
|
∴当a＞0时，f（a）＜0?log2a＜0，
解得：0＜a＜1；
当a＜0时，f（a）＜0?log
| 1 |
| 2 |
| 1 |
| 2 |
∴-x＞1，
解得：x＜-1．
∴实数a的取值范围是：（-∞，-1）∪（0，1）．
故答案为：（-∞，-1）∪（0，1）．
点评：本题考查对数不等式的解法，着重考查对数函数的单调性质，属于中档题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
不等式组
且u=x2+y2-4y，则u的最小值为（ ）
|
A、
| ||
| B、1 | ||
C、
| ||
| D、4 |
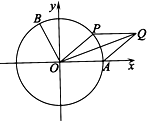如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且