Question

函数y=f（x）定义域为（

1

2

，+∞），f（1）=f（3）=1，f（x）的导数．f′（x）=a（

2

x

+2x-5），其中a为常数且a＞0，则不等式组

-2≤x-2y≤ 1 2 f(2x+y)≤1

所表示的平面区域的面积等于（　　）

• A、

  1

  5

• B、

  3

  5

• C、

  1

  2

• D、1

Answer 1

考点：二元一次不等式（组）与平面区域

专题：导数的综合应用,不等式的解法及应用

分析：根据导数确定函数的单调性和极值，然后根据函数的单调性解不等式组即可，利用二元一次不等式组表示平面区域，作出平面区域即可求出区域面积．

解答： 解：∵函数f（x）的定义域为（

1

2

，+∞），a＞0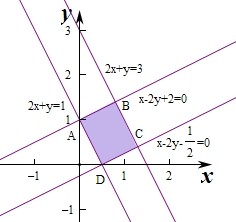
由f′（x）=a（

2

x

+2x-5）＞0，即2x²-5x+2＞0，解得x＞2，此时函数单调递增．
由f′（x）=a（

2

x

+2x-5）＜0，即2x²-5x+2＜0，解得

1

2

＜x＜2，此时函数单调递减．
即函数f（x）在x=2取得极小值，
∵f（1）=f（3）=1，要使f（2x+y）≤1，可得1≤2x+y≤3①，
结合-2≤x-2y≤

1

2

②画出满足条件①②的可行域如图：为矩形ABCD，
则A（0，1），
则AB等于点（0，1）到直线2x+y=3的距离：d=

|1-3|

1+4

=

2

5

，
另一条边等于AD=

|-2- 1 2 |

1+4

=

5 2

5

=

5

2

，
∴面积S=

2

5

×

5

2

=1，
故选D；

点评：本题主要考查线性规划问题，利用导数研究函数的单调性，找出可行域，是解决此题的关键，综合性较强．