题目内容
已知向量
=（sinθ，cosθ-2sinθ），
=（1，3）
（1）若
∥
，求tanθ的值；
（2）若|
-
|=|
+
|，求cos2θ的值．
| a |
| b |
（1）若
| a |
| b |
（2）若|
| a |
| b |
| a |
| b |
考点：平面向量数量积的坐标表示、模、夹角,三角函数中的恒等变换应用
专题：平面向量及应用
分析：（1）利用向量共线定理的坐标表示即可得出；
（2）由|
-
|=|
+
|，利用向量的平行四边形法则可得
⊥
，再利用向量垂直与数量积的关系及其三角函数的基本关系式即可得出．
（2）由|
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：（1）∵
∥
，
∴3sinθ-（cosθ-2sinθ）=0，化为5sinθ=cosθ，
∴tanθ=
．
（2）∵|
-
|=|
+
|，∴
⊥
，
∴
•
=sinθ+3（cosθ-2sinθ）=0，化为4sinθ=3cosθ，
又sin2θ+cos2θ=1，联立解得sinθ=±
．
∴cos2θ=1-2sin2θ=1-2×(±
)2=
．
| a |
| b |
∴3sinθ-（cosθ-2sinθ）=0，化为5sinθ=cosθ，
∴tanθ=
| 1 |
| 5 |
（2）∵|
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
又sin2θ+cos2θ=1，联立解得sinθ=±
| 3 |
| 5 |
∴cos2θ=1-2sin2θ=1-2×(±
| 3 |
| 5 |
| 7 |
| 25 |
点评：本题考查了向量共线定理的坐标表示即可得出、向量的平行四边形法则、向量垂直与数量积的关系及其三角函数的基本关系式，属于基础题．
练习册系列答案
相关题目
函数y=cos2x+2asinx在区间[-
，π]上的最大值为2，则实数a的值为（ ）
| π |
| 6 |
A、1或 -
| ||
B、-
| ||
C、
| ||
D、1或
|
点（-2，t）在直线2x-3y+6=0的上方，则t的取值范围是（ ）
A、t＞
| ||
B、t＜
| ||
C、t≥
| ||
D、0＜t＜
|
已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1．直径为4的球的体积为V2，则V1：V2=（ ）| A、1：4 | B、1：2 |
| C、1：1 | D、2：1 |
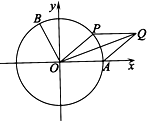如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且