题目内容
已知函数f(x)=
x2-alnx(a∈R).
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间;
(3)若a=-1,问:当x>1时,f(x)<
x3是否恒成立,并说明理由.
| 1 |
| 2 |
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间;
(3)若a=-1,问:当x>1时,f(x)<
| 2 |
| 3 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,确定切线的斜率,切点的坐标,即可求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)分类讨论,利用导数的正负,可求f(x)的单调区间;
(3)作差,利用函数的单调性,即可得出结论.
(2)分类讨论,利用导数的正负,可求f(x)的单调区间;
(3)作差,利用函数的单调性,即可得出结论.
解答:
解:f(x)的定义域为(0,+∞),…(1分)
由题意得f′(x)=x-
(x>0)…(2分)
(1)f'(1)=1-a,f(1)=
,
∴过点(1,f(1))处的切线方程为(1-a)x-y+a-
=0…(4分)
(2)当a≤0时,f(x)的单调递增区间为(0,+∞). …(5分)
当a>0时,f′(x)=x-
=
=
∴当0<x<
时,f′(x)<0; 当x>
时,f′(x)>0…(8分)
∴当a>0时,函数f(x)的单调递增区间为(
,+∞),单调递减区间为(0,
).…(9分)
(3)a=-1时,设g(x)=
x3-
x2-lnx(x>1),则g′(x)=2x2-x-
…(10分)
∵当x>1时,g'(x)=
>0,
∴g(x)在(1,+∞)上是增函数. …(12分)
∴g(x)>g(1)=
>0
即
x3-
x2-lnx>0,…(13分)
∴
x2+lnx<
x3
故当x>1时,
x2+lnx<
x3恒成立,即f(x)<
x3恒成立 …(14分)
由题意得f′(x)=x-
| a |
| x |
(1)f'(1)=1-a,f(1)=
| 1 |
| 2 |
∴过点(1,f(1))处的切线方程为(1-a)x-y+a-
| 1 |
| 2 |
(2)当a≤0时,f(x)的单调递增区间为(0,+∞). …(5分)
当a>0时,f′(x)=x-
| a |
| x |
| x2-a |
| x |
(x-
| ||||
| x |
∴当0<x<
| a |
| a |
∴当a>0时,函数f(x)的单调递增区间为(
| a |
| a |
(3)a=-1时,设g(x)=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
∵当x>1时,g'(x)=
| (x-1)(2x2+x+1) |
| x |
∴g(x)在(1,+∞)上是增函数. …(12分)
∴g(x)>g(1)=
| 1 |
| 6 |
即
| 2 |
| 3 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
故当x>1时,
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查导数知识的运用,考查利用导数研究曲线上某点切线方程,正确求导是关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
如果函数f(x+1)是偶函数,那么函数y=f(2x)的图象的一条对称轴是直线( )
| A、x=-1. | ||
| B、x=1 | ||
C、x=-
| ||
D、x=
|
 某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.
某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.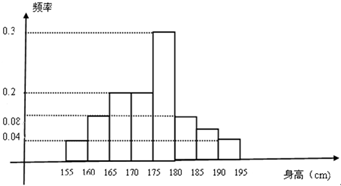 现从某校高三年年级学生中随机抽取n名同学测量身高,据测量,所有学生的身高均介于155至195cm之间,将测量结果按如下方式分成8组;第一组;[155,160);第二组[160,165);…,第八组[190,195].如图是按上述分组得到的条形图,其中第五组有15名同学.
现从某校高三年年级学生中随机抽取n名同学测量身高,据测量,所有学生的身高均介于155至195cm之间,将测量结果按如下方式分成8组;第一组;[155,160);第二组[160,165);…,第八组[190,195].如图是按上述分组得到的条形图,其中第五组有15名同学.