题目内容
已知点F(c,0)(c>0)是双曲线
-
=1的右焦点,F关于直线y=
x的对称点A恰在该双曲线的右支上,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出过焦点F且垂直直线y=
x的直线方程,联立直线y=
x,解方程组可得对称中心的点的坐标,代入方程结合a2+b2=c2,解出e即得.
| ||
| 3 |
| ||
| 3 |
解答:
解:过焦点F且垂直直线y=
x的直线方程为:y-0=-
(x-c),
联立直线y=
x,解之可得x=
c,y=
c
由中点坐标公式可得对称点的坐标为(
,
c),
将其代入双曲线的方程可得
-
=1,结合a2+b2=c2,
化简可得e4-8e2,+4=0,故可得e=
+1.
故选:A.
| ||
| 3 |
| 3 |
联立直线y=
| ||
| 3 |
| 3 |
| 4 |
| ||
| 4 |
由中点坐标公式可得对称点的坐标为(
| c |
| 2 |
| ||
| 2 |
将其代入双曲线的方程可得
| ||
| a2 |
| ||
| b2 |
化简可得e4-8e2,+4=0,故可得e=
| 3 |
故选:A.
点评:本题考查双曲线的简单性质,涉及离心率的求解和对称问题,属中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
函数在y=
定义域内( )
| 4x |
| x2+1 |
| A、有最大值2,无最小值 |
| B、无最大值,有最小值-2 |
| C、有最大值2,最小值-2 |
| D、无最值 |
在平面直角坐标系中,不等式
(a为常数)表示的平面区域的面积为8,则
的最小值为( )
|
| x+y+2 |
| x+3 |
A、8
| ||
B、5-4
| ||
C、6-4
| ||
D、
|
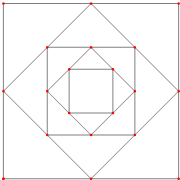 如图,画一个边长为10cm的正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了五个正方形,则它们的面积的和为( )
如图,画一个边长为10cm的正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了五个正方形,则它们的面积的和为( )| A、193.75cm2 |
| B、387.5cm2 |
| C、187.5cm2 |
| D、200.75cm2 |
在(x+y)n的展开式中,若第8项系数最大,则n的值可能等于( )
| A、14,15 |
| B、15,16 |
| C、16,17 |
| D、13,14,15 |
在△ABC中,
•
=
•
,则△ABC是( )
| CB |
| CA |
| BC |
| BA |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、直角三角形 |
已知函数f(x)=
,若存在实数t使得f(x)在R上为单调函数,则a的取值范围是( )
|
| A、a≥0 | B、a<0 |
| C、a≤t | D、a<-t |