题目内容
已知动点M到点F(0,1)的距离等于点M到直线y=-1的距离,点M的轨迹为C.
(Ⅰ)求轨迹C的方程;
(Ⅱ)设P为直线l:x-y-2=0上的点,过点P做曲线C的两条切线PA,PB,当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
(Ⅲ)当点P在直线l上移动时,求|AF|•|BF|的最小值.
(Ⅰ)求轨迹C的方程;
(Ⅱ)设P为直线l:x-y-2=0上的点,过点P做曲线C的两条切线PA,PB,当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
(Ⅲ)当点P在直线l上移动时,求|AF|•|BF|的最小值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)动点M到点F(0,1)的距离等于点M到直线y=-1的距离,根据抛物线的定义,可得结论;
(Ⅱ)求出切线PA,PB的方程,利用切线PA,PB均过P(x0,y0),可得A,B的坐标是方程x0x-2y-2y0=0的两组解,从而可求直线AB的方程;
(Ⅲ)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,表示出|AF|•|BF|,利用配方法可求|AF|•|BF|的最小值.
(Ⅱ)求出切线PA,PB的方程,利用切线PA,PB均过P(x0,y0),可得A,B的坐标是方程x0x-2y-2y0=0的两组解,从而可求直线AB的方程;
(Ⅲ)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,表示出|AF|•|BF|,利用配方法可求|AF|•|BF|的最小值.
解答:
解:(Ⅰ)∵动点M到点F(0,1)的距离等于点M到直线y=-1的距离,
∴根据抛物线的定义,可得抛物线的焦点F(0,1),
∴轨迹C的方程为x2=4y;
(Ⅱ)∵x2=4y,∴y=
x2,
∴y′=
x.
设A(x1,y1),B(x2,y2),则切线PA,PB的斜率分别为
x1,
x2,
∴切线PA的方程为y-y1=
x1(x-x1),即x1x-2y-2y1=0,
同理可得切线PB的方程为x2x-2y-2y2=0,
∵切线PA,PB均过点P(x0,y0),
∴x1x0-2y0-2y1=0,x2x0-2y0-2y2=0,
∴A(x1,y1),B(x2,y2)为方程x0x-2y0-2y=0的解,
∴直线AB的方程的方程为x0x-2y0-2y=0;
(Ⅲ)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,
∴|AF|•|BF|=(y1+1)(y2+1)=y1y2+(y1+y2)+1
由x0x-2y0-2y=0与抛物线的定义联立,可得y2+(2y0-x02)y+y02=0
∴|AF|•|BF|=y02+x02-2y0+1.
∵点P(x0,y0)在直线l上,
∴x0=y0+2,
∴|AF|•|BF|=y02+x02-2y0+1=2(y0+
)2+
,
∴当y0=-
时,|AF|•|BF|取得最小值,最小值为
.
∴根据抛物线的定义,可得抛物线的焦点F(0,1),
∴轨迹C的方程为x2=4y;
(Ⅱ)∵x2=4y,∴y=
| 1 |
| 4 |
∴y′=
| 1 |
| 2 |
设A(x1,y1),B(x2,y2),则切线PA,PB的斜率分别为
| 1 |
| 2 |
| 1 |
| 2 |
∴切线PA的方程为y-y1=
| 1 |
| 2 |
同理可得切线PB的方程为x2x-2y-2y2=0,
∵切线PA,PB均过点P(x0,y0),
∴x1x0-2y0-2y1=0,x2x0-2y0-2y2=0,
∴A(x1,y1),B(x2,y2)为方程x0x-2y0-2y=0的解,
∴直线AB的方程的方程为x0x-2y0-2y=0;
(Ⅲ)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,
∴|AF|•|BF|=(y1+1)(y2+1)=y1y2+(y1+y2)+1
由x0x-2y0-2y=0与抛物线的定义联立,可得y2+(2y0-x02)y+y02=0
∴|AF|•|BF|=y02+x02-2y0+1.
∵点P(x0,y0)在直线l上,
∴x0=y0+2,
∴|AF|•|BF|=y02+x02-2y0+1=2(y0+
| 1 |
| 2 |
| 9 |
| 2 |
∴当y0=-
| 1 |
| 2 |
| 9 |
| 2 |
点评:本题考查轨迹方程,考查抛物线的切线方程,考查韦达定理的运用,考查学生的计算能力,属于难题.

练习册系列答案
相关题目
已知锐角A,B满足2tanA=tan(A+B),则tanB的最大值为( )
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.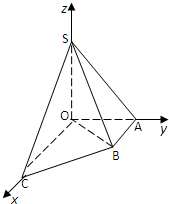 如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz. 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.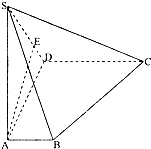 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.