题目内容

已知向量
a
=(1，-2)，
b
=(x，4)，且
a
∥
b
，则|
a
-
b
|=（　　）
A、5
3
B、3
5
C、2
5
D、2
2
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：利用向量向量共线定理可得x，再利用向量模的计算公式即可得出．
解答： 解：∵
a
∥
b
，∴-2x-4=0，解得x=-2．
∴
a
-
b
=（1，-2）-（-2，4）=（3，-6）．
∴|
a
-
b
|=
32+(-6)2
=3
5
．
故选：B．
点评：本题考查平面向量的基本运算，属于基础题．
练习册系列答案
相关题目
设F1，F2是双曲线C：
x2
16
-
y2
b2
=1(b＞0)的两个焦点，P是双曲线C上一点，若∠F1PF2=90°且△PF1F2的面积为9，则C的离心率为
 
．
给出下列命题：
（1）若
a
•
b
=
a
•
c
，则
b
=
c
；
（2）对空间任意点O与不共线的三点A，B，C，若
OP
=x
OA
+y
OB
+z
OC
（x，y，z∈R），则P，A，B，C四点共面；
（3）“曲线C上的点的坐标都是方程f（x，y）=0的解”是“曲线C的方程是f（x，y）=0”的必要条件；
（4）（
c
•
b
）
a
-（
a
•
c
）
b
与
c
垂直．
写出以上命题为真命题的序号
 
．
设Sn为等差数列{an}的前n项和，已知S5=5，S9=27，则S7=
 
．
若函数f（x）=2sin（
π
8
x+
π
4
）（-2＜x＜14）的图象与x轴交于点A，过点A的直线l与函数的图象交于B、C两点，则（
OB
+
OC
）•
OA
=（其中O为坐标原点）（　　）
A、-32B、32
C、-72D、72
已知锐角A，B满足2tanA=tan（A+B），则tanB的最大值为（　　）
A、2
2
B、
2
C、
2
2
D、
2
4
己知某几何体的三视图如图所示，则该几何体的体积是（　　）
A、
2
3
3
+π
B、
2
3
3
+2π
C、2
3
+2π
D、2
3
+π
已知F是双曲线
x2
3a2
-
y2
a2
=1(a＞0)的右焦点，O为坐标原点，设P是双曲线C上一点，则∠POF的大小不可能是（　　）
A、15°B、25°
C、60°D、165°
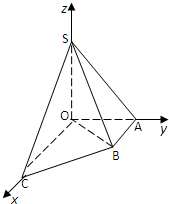如图直角梯形OABC中，∠COA=∠OAB=90°，OC=2，OA=AB=1，SO⊥平面OABC，SO=1，分别以OC，OA，OS为x轴、y轴、z轴建立直角坐标系O-xyz．
（Ⅰ）求
SC
与
OB
夹角的余弦值；
（Ⅱ）求OC与平面SBC夹角的正弦值；
（Ⅲ）求二面角S-BC-O．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网