题目内容
4.抛物线y2=2x与直线y=x-4围成的平面图形面积( )| A. | 18 | B. | 16 | C. | 20 | D. | 14 |
分析 方法一:根据题目信息,作出图形,如图所示:联立$\left\{\begin{array}{l}{y=2x}\\{y=x-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,则所求的面积为S=${∫}_{0}^{2}$$\sqrt{2x}$dx+${∫}_{2}^{8}$($\sqrt{2x}$-x+4)dx,求出原函数,即可求得平面区域的面积,方法二:对y进行积分,所求的面积为S=${∫}_{-2}^{4}$(y+4-$\frac{{y}^{2}}{2}$)dy,即可求得平面区域的面积.
解答 解:方法一:根据题目信息,作出图形,如图所示: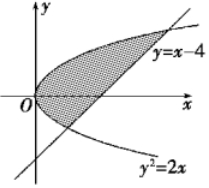
联立$\left\{\begin{array}{l}{y=2x}\\{y=x-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,则所求的面积为S=${∫}_{0}^{2}$$\sqrt{2x}$dx+${∫}_{2}^{8}$($\sqrt{2x}$-x+4)dx.
∵[$\frac{1}{3}$•$(2x)^{\frac{3}{2}}$]′=$\sqrt{2x}$,
∴S=[$\frac{1}{3}$•$(2x)^{\frac{3}{2}}$]${丨}_{0}^{2}$+[$\frac{1}{3}$•$(2x)^{\frac{3}{2}}$-$\frac{{x}^{2}}{2}$+4x]${丨}_{2}^{8}$=18
故抛物线y2=2x与直线y=x-4所围成的图形的面积是18,
故选A.
方法二:根据题目信息,作出图形,如图所示:
联立$\left\{\begin{array}{l}{y=2x}\\{y=x-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,
则所求的面积为S=${∫}_{-2}^{4}$(y+4-$\frac{{y}^{2}}{2}$)dy=($\frac{1}{2}$y2+4y-$\frac{{y}^{3}}{6}$)${丨}_{-2}^{4}$=(8+16-$\frac{32}{3}$-2+8-$\frac{4}{3}$)=18,
故选A.
点评 本题考查定积分的简单应用,考查抛物线的与直线的位置关系,考查计算能力,选择合适的积分函数能够减少计算量,属于中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | p是假命题 | B. | q是真命题 | C. | p∧(¬q)是真命题 | D. | (¬p)∧q是真命题 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | ϕ | B. | {1,2} | C. | {-1,1,2} | D. | {2} |
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2>b2 | C. | a+b≥2$\sqrt{ab}$ | D. | a2+b2>2ab |