题目内容
9.P是双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的右支上一点,M,N分别是圆x2+y2+10x+21=0和x2+y2-10x+24=0上的点,则|PM|-|PN|的最大值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由题设通过双曲线的定义推出|PF1|-|PF2|=6,利用|MP|≤|PF1|+|MF1|,|PN|≥|PF2|-|NF2|,推出|PM|-|PN|≤|PF1|+|MF1|-|PF2|-|NF2|,求出最大值.
解答 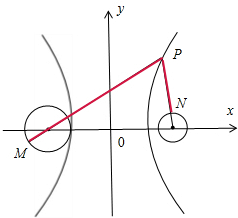 解:双曲线双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$,如图:
解:双曲线双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$,如图:
∵a=3,b=4,c=5,
∴F1(-5,0),F2(5,0),
∵x2+y2+10x+21=0,x2+y2-10x+24=0,
∴(x+5)2+y2=4和(x-5)2+y2=1,
∵|PF1|-|PF2|=2a=6,
∴|MP|≤|PF1|+|MF1|,|PN|≥|PF2|-|NF2|,
∴-|PN|≤-|PF2|+|NF2|,
所以,|PM|-|PN|≤|PF1|+|MF1|-|PF2|+|NF2|
=6+1+2
=9.
故选D
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
20.集合A={α|α=kπ+$\frac{π}{2}$,k∈Z}与集合B={α|α=2kπ±$\frac{π}{2}$,k∈Z}的关系是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | 以上都不对 |
17.在等差数列{an}中,a1=2,公差为d,则“d=2”是“a1,a2,a4成等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.抛物线y2=2x与直线y=x-4围成的平面图形面积( )
| A. | 18 | B. | 16 | C. | 20 | D. | 14 |
14.已知2a=5b=m且$\frac{1}{a}+\frac{1}{b}$=2,则m的值是( )
| A. | 100 | B. | 10 | C. | $\sqrt{10}$ | D. | $\frac{1}{10}$ |
1.已知{an}是等比数列,a2=2,a4=8,则a6=( )
| A. | 4 | B. | 16 | C. | 32 | D. | 64 |
18.已知$\frac{π}{4}<α<\frac{3π}{4}$,$sin(α-\frac{π}{4})=\frac{4}{5}$,则cosα=( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{\sqrt{2}}}{5}$ |