题目内容
设函数f(x)=|x+3|-|x-1|.
(Ⅰ)解不等式f(x)≤1;
(Ⅱ)若存在x0,使得f(x0)≥log2a成立,求a的取值范围.
(Ⅰ)解不等式f(x)≤1;
(Ⅱ)若存在x0,使得f(x0)≥log2a成立,求a的取值范围.
考点:分段函数的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)将f(x)=|x+3|-|x-1|化为分段函数,由此解不等式,即可得到;
(Ⅱ)存在x0,使得f(x0)≥log2a成立,等价于f(x)max≥log2a,由(Ⅰ)可知,log2a≤4,解出不等式即可.
(Ⅱ)存在x0,使得f(x0)≥log2a成立,等价于f(x)max≥log2a,由(Ⅰ)可知,log2a≤4,解出不等式即可.
解答:
解:(Ⅰ)f(x)=|x+3|-|x-1|
=
即
由f(x)≤1则x<-3或
,
解得x<-3或-3≤x≤-
,
故不等式的解集为(-∞,-
].
(Ⅱ)存在x0,使得f(x0)≥log2a成立,等价于f(x)max≥log2a,
由(Ⅰ)可知,log2a≤4,解得0<a≤16.
故a的取值范围是(0,16].
=
|
|
由f(x)≤1则x<-3或
|
解得x<-3或-3≤x≤-
| 1 |
| 2 |
故不等式的解集为(-∞,-
| 1 |
| 2 |
(Ⅱ)存在x0,使得f(x0)≥log2a成立,等价于f(x)max≥log2a,
由(Ⅰ)可知,log2a≤4,解得0<a≤16.
故a的取值范围是(0,16].
点评:本题考查绝对值函数及运用,考查函数的最值,及存在性问题转化为求函数的最值问题,考查运算能力,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
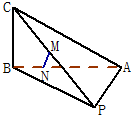 已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.
已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.