Question

15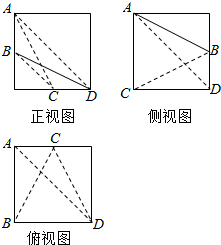．已知，棱长为2的正方体内有一内接四面体A-BCD，且B，C分别为正方体某两条棱的中点，其三视图如图所示：
（Ⅰ）求证：AD⊥BC；
（Ⅱ）求四面体A-BCD的体积．

Answer 1

分析 （Ⅰ）根据已知中的三视图，确定A，B，C，D四点的位置，令E为AD的中点，连接BE，CE，证明AD⊥平面BCE，即可证明AD⊥BC；
（Ⅱ）利用割补法，可求出四面体A-BCD的体积．

解答 （Ⅰ）证明：由已知中的三视图，可得A，B，C，D四点位置如下图所示：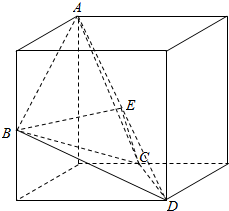

∵正方体的棱长为2，故AB=BD=AC=CD=$\sqrt{5}$，AD=2$\sqrt{3}$，BC=$\sqrt{6}$，
令E为AD的中点，连接BE，CE，
则BE⊥AD，CE⊥AD，
则AD⊥平面BCE，
∴AD⊥BC；
（Ⅱ）解：由勾股定理可得：BE=CE=$\sqrt{2}$，
由海伦公式平面BCE的面积S=$\frac{\sqrt{3}}{2}$，
又由AD=2$\sqrt{3}$，
故四面体A-BCD的体积V=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=1．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．