题目内容
10.若函数f(x)=lg[(1-a2)x2+4(a-1)x+4]值域为R,求实数a满足的条件.分析 根据对数函数的性质建立不等式关系进行求解即可.
解答 解:∵函数f(x)=lg[(1-a2)x2+4(a-1)x+4]的值域为R,
∴当1-a2=0时,得a=1或a=-1,
当a=1时,f(x)=lg4,函数的值域为{lg4},不满足条件.
当a=-1时,f(x)=lg(4-8x),此时函数的值域为R,满足条件.
当a≠±1,
设y=(1-a2)x2+4(a-1)x+4,
要使函数f(x)的值域为R,
则满足二次项系数1-a2>0,即-1<a<1
根的判别式△=16(a-1)2-16(1-a2)≥0,
即2a(a-1)≥0,解得a≥1或a≤0,
∵-1<a<1
∴此时-1<a≤0.
综上-1≤a≤0.
点评 本题考查了函数的值域,还考查了分类讨论的数学思想,根据对数函数的性质结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
8.总体由编号为00,01,02,…,19的20个个体组成,利用下面给出的随机数表从20个个体中选取5个个体,选取方法是从随机数表第一行的第5列数字开始由左到右依次选定两个数字,则选出来的第5个个体编号为( )
| 78 | 16 | 95 | 72 | 08 | 14 | 07 | 43 | 63 | 42 | 03 | 20 | 97 | 28 | 01 | 98 |
| 32 | 04 | 92 | 34 | 49 | 35 | 82 | 40 | 36 | 23 | 48 | 69 | 69 | 38 | 74 | 81 |
| A. | 01 | B. | 07 | C. | 08 | D. | 20 |
9.在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=AA1,则异面直线AC1与B1C所成角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,过EF的截面EFG与底面成60°二面角,且与棱AA1交于G,求棱锥G-AEF的体积.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,过EF的截面EFG与底面成60°二面角,且与棱AA1交于G,求棱锥G-AEF的体积. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.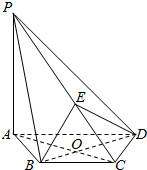 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,