题目内容
1.函数$y=\sqrt{\frac{x-3}{2-x}}$的定义域是( )| A. | {x|2≤x≤3} | B. | {x|x≤2或x≥3} | C. | {x|2<x≤3} | D. | {x|x<2或x≥3} |
分析 根据函数的定义域的条件即可求出
解答 解:要使$y=\sqrt{\frac{x-3}{2-x}}$有意义,则$\frac{x-3}{2-x}$≥0,即(x-3)(x-2)≤0,且x≠2,解得2<x≤3,
故函数的定义域为:{x|2<x≤3},
故选:C
点评 本题考查了函数的定义域,属于基础题

练习册系列答案
相关题目
9.华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如表:(单位:人)
(1)在犯错误的概率不超过1%的条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间为5-8分钟,乙每次解答一道物理题所用的时间为6-8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对他们的解答情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列和数学期望.
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 物理题 | 数学题 | 总计 | |
| 男同学 | 16 | 14 | 30 |
| 女同学 | 8 | 22 | 20 |
| 总计 | 24 | 36 | 60 |
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间为5-8分钟,乙每次解答一道物理题所用的时间为6-8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对他们的解答情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列和数学期望.
附表及公式:
| P(K2?k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16.${log_2}8+{log_2}\frac{1}{2}$=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.六位同学站成一排照毕业相,甲同学和乙同学要求相邻,并且都不和丙丁相邻,则一共有多种排法( )
| A. | 72 | B. | 144 | C. | 180 | D. | 288 |
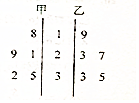 甲、乙两组数据的茎叶图如图所示,则平均数较小的一组数为甲.(选填“甲”或“乙”)
甲、乙两组数据的茎叶图如图所示,则平均数较小的一组数为甲.(选填“甲”或“乙”)