题目内容
已知函数f(x)=
.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若方程f(x)=
有解,求实数m的取值范围;
(Ⅲ)若存在实数x1≠x2,使x1•f(x1)=x2•f(x2)成立,求证:x1+x2>6.
| x2 |
| ex |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若方程f(x)=
| m |
| x |
(Ⅲ)若存在实数x1≠x2,使x1•f(x1)=x2•f(x2)成立,求证:x1+x2>6.
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)先求导数,然后解不等式f′(x)>0、f′(x)<0可得单调区间;
(Ⅱ)f(x)=
?m=
(x≠0),令g(x)=
(x≠0),利用导数可求得g(x)的范围,即得m的范围;
(Ⅲ)反证法:令h(x)=xf(x)=
(x∈R),由(2)知,h(x)的单调性,由条件知h(x1)=h(x2),不妨设x1<x2,则必有x1<3,x2>3,于是6-x2<3,假设x1+x2≤6,利用单调性、导数可推出矛盾;
(Ⅱ)f(x)=
| m |
| x |
| x3 |
| ex |
| x3 |
| ex |
(Ⅲ)反证法:令h(x)=xf(x)=
| x3 |
| ex |
解答:
解:(Ⅰ)f′(x)=(2x-x2)e-x,
令f′(x)>0,得0<x<2,f′(x)<0,得x<0或x>2,
∴f(x)的递增区间为(0,2),递减区间为(-∞,0),(2,+∞);
(Ⅱ)f(x)=
?m=
(x≠0),
令g(x)=
(x≠0),则g′(x)=(3x2-x3)e-x,
令g′(x)>0,得x<3,g′(x)<0,得x>3,
∴g(x)在(-∞,0),(0,3)上递增,在(3,+∞)上递减,
∴g(x)max=g(3)=
,
故m∈(-∞,0)∪(0,
];
(Ⅲ)令h(x)=xf(x)=
(x∈R),则由(2)知,h(x)在(-∞,3)上递增,在(3,+∞)上递减.
由条件知h(x1)=h(x2),不妨设x1<x2,则必有x1<3,x2>3,于是6-x2<3,
假设x1+x2≤6,则x1≤6-x2⇒h(x1)≤h(6-x2),即h(x2)≤h(6-x2)?
≤
?
≤
,
令3-x2=t(t<0),
则有
≤(
)3?e
≤
(t<0),即(3-t)e
-t-3≤0 (*),
令u(x)=(3-x)e
-x-3(x<0).u′(x)=(1-
)e
-1,
因为u′(x)=-
xe
>0(x<0)恒成立,所以u′(x)在(-∞,0)上是增函数,
所以u′(x)<u′(0)=0,所以u(x)在(-∞,0)上是减函数,
故u(x)>u(0)=0,∴t<0时,u(t)>0,这与(*)矛盾!
所以原不等式得证,即x1+x2>6.
令f′(x)>0,得0<x<2,f′(x)<0,得x<0或x>2,
∴f(x)的递增区间为(0,2),递减区间为(-∞,0),(2,+∞);
(Ⅱ)f(x)=
| m |
| x |
| x3 |
| ex |
令g(x)=
| x3 |
| ex |
令g′(x)>0,得x<3,g′(x)<0,得x>3,
∴g(x)在(-∞,0),(0,3)上递增,在(3,+∞)上递减,
∴g(x)max=g(3)=
| 27 |
| e3 |
故m∈(-∞,0)∪(0,
| 27 |
| e3 |
(Ⅲ)令h(x)=xf(x)=
| x3 |
| ex |
由条件知h(x1)=h(x2),不妨设x1<x2,则必有x1<3,x2>3,于是6-x2<3,
假设x1+x2≤6,则x1≤6-x2⇒h(x1)≤h(6-x2),即h(x2)≤h(6-x2)?
| x23 |
| ex2 |
| (6-x2)3 |
| e6-x2 |
| e6-x2 |
| ex2 |
| (6-x2)3 |
| x23 |
令3-x2=t(t<0),
则有
| e3+t |
| e3-t |
| 3+t |
| 3-t |
| 2t |
| 3 |
| 3+t |
| 3-t |
| 2t |
| 3 |
令u(x)=(3-x)e
| 2x |
| 3 |
| 2x |
| 3 |
| 2x |
| 3 |
因为u′(x)=-
| 4 |
| 9 |
| 2x |
| 3 |
所以u′(x)<u′(0)=0,所以u(x)在(-∞,0)上是减函数,
故u(x)>u(0)=0,∴t<0时,u(t)>0,这与(*)矛盾!
所以原不等式得证,即x1+x2>6.
点评:本题考查利用导数研究函数的单调性、极值最值,考查不等式的证明,反证法是证明(Ⅲ)问的关键所在,该题综合性强,能力要求较高.

练习册系列答案
相关题目
若函数y=x3-ax2+4在区间(0,2)内是单调递减函数,则实数a的取值范围是( )
| A、a≥3 | B、a=3 |
| C、a≤3 | D、0<a<3 |
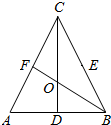 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量 如图,在平行四边形ABCD中,|AB|=3,|BC|=2,
如图,在平行四边形ABCD中,|AB|=3,|BC|=2,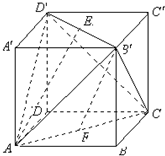 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: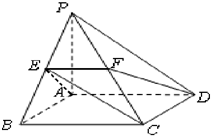 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.