题目内容
 在Rt△AOB中,∠OAB=
在Rt△AOB中,∠OAB=| π |
| 6 |
(1)求证:平面COD⊥平面AOB;
(2)当AD=
| 1 |
| 2 |
(3)求CD与平面AOB所成最大角的正切值.
考点:直线与平面所成的角,异面直线及其所成的角,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用二面角的定义、线面与面面垂直的判定与性质即可得出;
(2)作DE⊥OB,垂足为E,连结CE,则DE∥AO,∠CDE是异面直线AO与CD所成的角,在Rt△CDE中,可求异面直线AO与CD所成角的正切值;
(3)由(1)知,CO⊥平面AOB,可得∠CDO是CD与平面AOB所成的角,当OD最小时,∠CDO最大,结合含30°角的直角三角形的边角关系即可得出.
(2)作DE⊥OB,垂足为E,连结CE,则DE∥AO,∠CDE是异面直线AO与CD所成的角,在Rt△CDE中,可求异面直线AO与CD所成角的正切值;
(3)由(1)知,CO⊥平面AOB,可得∠CDO是CD与平面AOB所成的角,当OD最小时,∠CDO最大,结合含30°角的直角三角形的边角关系即可得出.
解答:
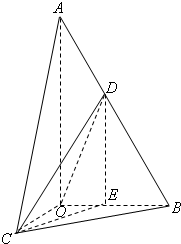 (1)证明:由题意,CO⊥AO,BO⊥AO,
(1)证明:由题意,CO⊥AO,BO⊥AO,
∴∠BOC是直二面角B-AO-C的平面角,…(2分)
∴CO⊥BO,
又∵AO∩BO=O,∴CO⊥平面AOB,
又CO?平面COD,
∴平面COD⊥平面AOB. …(4分)
(2)解:作DE⊥OB,垂足为E,连结CE,则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角. …(6分)
在 Rt△COB中,易得CO=BO=2,OE=
BO=
,
∴CE=
=
.
又DE=
AO=
.
∴在Rt△CDE中,tan∠CDE=
=
.
∴异面直线AO与CD所成角的正切值为
. …(9分)
(3)解:由(1)知,CO⊥平面AOB,∴∠CDO是CD与平面AOB所成的角,且tan∠CDO=
=
.
当OD最小时,∠CDO最大,…(11分)
这时,OD⊥AB,垂足为D,OD=
=
,tan∠CDO=
,
∴CD与平面AOB所成最大角的正切值为
.…(14分)
 (1)证明:由题意,CO⊥AO,BO⊥AO,
(1)证明:由题意,CO⊥AO,BO⊥AO,∴∠BOC是直二面角B-AO-C的平面角,…(2分)
∴CO⊥BO,
又∵AO∩BO=O,∴CO⊥平面AOB,
又CO?平面COD,
∴平面COD⊥平面AOB. …(4分)
(2)解:作DE⊥OB,垂足为E,连结CE,则DE∥AO,
∴∠CDE是异面直线AO与CD所成的角. …(6分)
在 Rt△COB中,易得CO=BO=2,OE=
| 1 |
| 3 |
| 2 |
| 3 |
∴CE=
| CO2+OE2 |
2
| ||
| 3 |
又DE=
| 2 |
| 3 |
4
| ||
| 3 |
∴在Rt△CDE中,tan∠CDE=
| CE |
| DE |
| ||
| 6 |
∴异面直线AO与CD所成角的正切值为
| ||
| 6 |
(3)解:由(1)知,CO⊥平面AOB,∴∠CDO是CD与平面AOB所成的角,且tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
当OD最小时,∠CDO最大,…(11分)
这时,OD⊥AB,垂足为D,OD=
| OA•OB |
| AB |
| 3 |
2
| ||
| 3 |
∴CD与平面AOB所成最大角的正切值为
2
| ||
| 3 |
点评:熟练掌握二面角的定义、线面与面面垂直的判定与性质、线面角的定义及其含30°角的直角三角形的边角关系是解题的关键.

练习册系列答案
相关题目
一条直线与一个平面垂直的条件是( )
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |
 如图,在平行四边形ABCD中,|AB|=3,|BC|=2,
如图,在平行四边形ABCD中,|AB|=3,|BC|=2,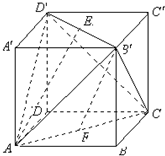 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: