题目内容
在一个三角形的三边长之比为3：5：7，则其最大的角是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：正弦定理
专题：解三角形
分析：根据大边对大角，利用余弦定理求得最大边对应角的余弦值，可得最大角．
解答：
解：设三边长为3x，5x，7x，则由大边对大角可得7x对应的角θ最大，
利用余弦定理可得 cosθ=
=-
，
∴θ=
，
故选：B．
利用余弦定理可得 cosθ=
| (3x)2+(5x)2-(7x)2 |
| 2•3x•5x |
| 1 |
| 2 |
∴θ=
| 2π |
| 3 |
故选：B．
点评：此题主要考查余弦定理的应用，大边对大角，根据三角函数的值求角，属于基础题．
练习册系列答案
相关题目
方程x3-3x2+1=0的实根的个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
已知l，m，n为互不重合的三条直线，平面α⊥平面β，α∩β=l，m?α，n?β，那么m⊥n是m⊥β的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若函数y=x3-ax2+4在区间（0，2）内是单调递减函数，则实数a的取值范围是（ ）
| A、a≥3 | B、a=3 |
| C、a≤3 | D、0＜a＜3 |
给出下列命题：
①函数y=2-|x|为偶函数；
②函数y=1是周期函数；
③函数f（x）=2x-x2的零点有2个；
④函数g（x）=|log2x|-（
）x在（0，+∞）上恰有两个零点x1，x2且x1•x2＜1．
其中正确命题的个数是（ ）
①函数y=2-|x|为偶函数；
②函数y=1是周期函数；
③函数f（x）=2x-x2的零点有2个；
④函数g（x）=|log2x|-（
| 1 |
| 2 |
其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
一条直线与一个平面垂直的条件是（ ）
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |
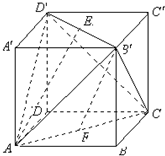正方体ABCD-A′B′C′D′的棱长等于2，E，F分别是B′D′，AC的中点．求：