题目内容
20.已知数列{an}为等差数列,a1=sinθ(-$\frac{π}{2}$≤θ≤$\frac{π}{2}$),a5=a3+1,且其前10项和S10=$\frac{55}{2}$.(1)求θ的值;
(2)求数列bn=an+($\frac{1}{2}$)${\;}^{2{a}_{n}}$的前n项和.
分析 (1)通过a5=a3+1可知d=$\frac{1}{2}$,进而结合S10=$\frac{55}{2}$可知a1=$\frac{1}{2}$,进而结合三角函数的单调性可知θ的值为$\frac{π}{6}$;
(2)通过(1)可知an=$\frac{n}{2}$,bn=$\frac{n}{2}$+$\frac{1}{{2}^{n}}$,利用分组求和法计算即得结论.
解答 解:(1)记等差数列{an}的公差为d,则由a5=a3+1可知1=a5-a3=2d,即d=$\frac{1}{2}$,
由S10=$\frac{55}{2}$=10a1+$\frac{10×9}{2}$×$\frac{1}{2}$可知a1=$\frac{1}{2}$,
又a1=sinθ(-$\frac{π}{2}$≤θ≤$\frac{π}{2}$),
所以θ的值为$\frac{π}{6}$;
(2)由(1)可知an=$\frac{n}{2}$,bn=an+($\frac{1}{2}$)${\;}^{2{a}_{n}}$=$\frac{n}{2}$+$\frac{1}{{2}^{n}}$,
所以所求值为$\frac{1}{2}$×$\frac{n(n+1)}{2}$+$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=$\frac{n(n+1)}{4}$-$\frac{1}{{2}^{n}}$+1.
点评 本题考查数列的通项及前n项和,考查三角函数的单调性及求值,考查分组法求和,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在△ABC中,点M为边BC上任意一点,点N为AM的中点,若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
11.已知集合A={x|1<x<3},B={x|y=log2(2-x)},则A∩B=( )
| A. | (0,3) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
15.设复数z满足z2=3+4i(i是虚数单位),则z的模为( )
| A. | 25 | B. | 5 | C. | $\sqrt{5}$ | D. | 2+i |
5.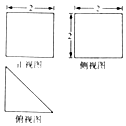 在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )
 在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )| A. | 9π:2:1 | B. | 3$\sqrt{3}$π:3:1 | C. | 3$\sqrt{3}$π:2:1 | D. | 3$\sqrt{3}$π:1:1 |
10.设集合A={-1,0,1},B={x|x2-2x-3≤0},则A∩B=( )
| A. | {-1,0,1} | B. | {0} | C. | (-1,1) | D. | (-1,3) |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的左焦点F与抛物线y2=-4x的焦点重合,直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的左焦点F与抛物线y2=-4x的焦点重合,直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.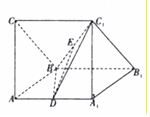 在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.