题目内容
设实数x，y满足
，则x+y=（ ）
|
| A、0 | B、3 | C、6 | D、9 |
考点：正弦函数的奇偶性,函数奇偶性的性质
专题：函数的性质及应用,三角函数的求值
分析：首先把关系是恒等变换变换成同形函数，进一步利用奇偶性和单调性进行求解．
解答：
解：根据上面的关系式：3（x-3）3+2x-sin（x-3）=9
转化为：3（x-3）3+2（x-3）-sin（x-3）=3
3（y-3）3+2y-sin（y-3）=3
转化为：3（y-3）3+2（y-3）-sin（y-3）=-3
设函数f（t）=3t3+2t-sint
则f（t）为奇函数
f′（t）=9t2+2-cost＞0
函数f（t）为增函数．
所以：f（x-3）=3 f（y-3）=-3
所以：f（x-3）=f（3-y）
根据函数f（t）为增函数．
所以：x-3=3-y
即x+y=6
故选：C
转化为：3（x-3）3+2（x-3）-sin（x-3）=3
3（y-3）3+2y-sin（y-3）=3
转化为：3（y-3）3+2（y-3）-sin（y-3）=-3
设函数f（t）=3t3+2t-sint
则f（t）为奇函数
f′（t）=9t2+2-cost＞0
函数f（t）为增函数．
所以：f（x-3）=3 f（y-3）=-3
所以：f（x-3）=f（3-y）
根据函数f（t）为增函数．
所以：x-3=3-y
即x+y=6
故选：C
点评：本题考查的知识要点：函数的就行与单调性的应用，函数关系式的恒等变形，导数在单调性中的应用．
练习册系列答案
相关题目
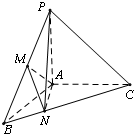如图，在三棱锥P-ABC中，PA⊥面ABC，∠BAC=120°，且AB=AC=AP，M为PB的中点，N在BC上，且BN=| 1 |
| 3 |
（1）求证：MN⊥AB；
（2）求平面MAN与平面PAN的夹角的余弦值．
设集合M={x|x＞
}，则下面式子正确的是（ ）
| 3 |
| A、φ⊆M | ||
| B、0∈M | ||
C、-
| ||
| D、2∉M |