题目内容

设x∈R，比较1+2x4与x2+2x3的大小．
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用“作差法”即可得出．
解答： 解：1+2x4-（x2+2x3）
=（1-x2）-2x3（1-x）
=（1-x）（1+x-2x3）
=（1-x）2（1+2x+2x2）
≥0，
∴1+2x4≥x2+2x3．
点评：本题考查了利用“作差法”比较两个数的大小方法，属于基础题．
练习册系列答案
相关题目
函数y=|x-1|+1的图象的对称轴方程为（　　）
A、x=1B、x=-1
C、y=1D、y=-1
设函数f（x）=sin（2x+φ）（-π＜φ＜0），y=f（x）图象的一条对称轴是直线x=
π
8
．
（1）求φ；
（2）由正弦曲线经过怎样的变换得到f（x）的图象．
函数f（x）=-2cosx+1，y=f'（x）在区间[a，b]上是增函数且f'（a）=-1，f'（b）=1，则f（
a+b
2
）等于（　　）
A、0
B、
2
2
C、1
D、-1
写出命题“若a＜b，则ac2＜bc2”的逆命题，否命题，逆否命题．
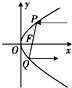为了研究探照灯的结构特征，在坐标轴中画出了探照灯的轴截面，如图．已知探照灯的轴截面图是抛物线y2=2px（p＞0）的一部分，若该抛物线的焦点恰好在直线x+y-1=0上．
（1）求该抛物线的方程；
（2）若一束平行于x轴的直线入射到抛物线的P点，经过抛物线焦点F后，由点Q反射出平行光线，试确定点P的位置使得从入射点P到反射点Q的路程最短．
已知函数f（x）=ax2-ln x．
（1）求函数的单调区间与最值；
（2）当a=1时，函数g（x）=1-
f(x)
x2
，求证：
ln2
24
+
ln3
34
+…+
lnn
n4
＜
1
2e
．（其中e为自然对数的底数）
已知数列{an}满足：a1=a2-2a+2，an+1=an+2（n-a）+1，n∈N+，当且仅当n=3时an最小，则实数a的取值范围为 （　　）
A、（-1，3）
B、(
5
2
，3)
C、（2，4）
D、(
5
2
，
7
2
)
设x＞-1，求函数y=
(x+5)(x+2)
x+1
的最值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网