题目内容
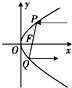 为了研究探照灯的结构特征,在坐标轴中画出了探照灯的轴截面,如图.已知探照灯的轴截面图是抛物线y2=2px(p>0)的一部分,若该抛物线的焦点恰好在直线x+y-1=0上.
为了研究探照灯的结构特征,在坐标轴中画出了探照灯的轴截面,如图.已知探照灯的轴截面图是抛物线y2=2px(p>0)的一部分,若该抛物线的焦点恰好在直线x+y-1=0上.(1)求该抛物线的方程;
(2)若一束平行于x轴的直线入射到抛物线的P点,经过抛物线焦点F后,由点Q反射出平行光线,试确定点P的位置使得从入射点P到反射点Q的路程最短.
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)直线x+y-1=0与x轴的交点为(1,0)点的焦点坐标,即可求解抛物线方程.
(2)设点P坐标为(
,a)(a≠0),推出PQ的方程为y=
(x-1).与抛物线方程联立,求出Q的坐标,利用|PQ|=|PF|+|QF|=
+
+2以及基本不等式求出最值,即可点的入射点P到反射点Q的路程最短.
(2)设点P坐标为(
| a2 |
| 4 |
| 4a |
| a2-4 |
| a2 |
| 4 |
| 4 |
| a2 |
解答:
解:(1)直线x+y-1=0与x轴的交点为(1,0),
故抛物线焦点F(1,0),抛物线方程为y2=4x. (5分)
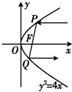
(2)设点P坐标为(
,a)(a≠0),又PQ过焦点可得PQ的方程为y=
(x-1).
由
解得y=a或y=-
,
故点Q(
,-
),则|PQ|=|PF|+|QF|=
+
+2≥2+2=4,
当且仅当a=±2时,取等号,
故当点P的坐标为(1,2)或(1,-2)时,从入射点P到反射点Q的路程最短为4. (12分)
故抛物线焦点F(1,0),抛物线方程为y2=4x. (5分)

(2)设点P坐标为(
| a2 |
| 4 |
| 4a |
| a2-4 |
由
|
| 4 |
| a |
故点Q(
| 4 |
| a2 |
| 4 |
| a |
| a2 |
| 4 |
| 4 |
| a2 |
当且仅当a=±2时,取等号,
故当点P的坐标为(1,2)或(1,-2)时,从入射点P到反射点Q的路程最短为4. (12分)
点评:本题考查抛物线与直线的位置关系,抛物线方程的求法,考查基本不等式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知抛物线y2=2px(p>0)上一点P到焦点F的距离为p,到x轴的距离为1,过F作倾斜角为45°的直线l与抛物线的准线交于点A,则
•
等于( )
| OA |
| OF |
A、-
| ||
B、-
| ||
C、
| ||
D、
|