题目内容
9.已知函数$f(x)=lnx-ax+\frac{1-a}{x}-1$.(1)若f(x)在x=2处取得极值,求a的值;
(2)若a=1,函数$h(x)=ln(m{x^2}+\frac{x}{2})+\frac{{-2{x^2}-x+2}}{2x+1}-f(x)$,且h(x)在(0,+∞)上的最小值为2,求实数m的值.
分析 (1)求出函数的导数,计算f′(2)=0,求出a的值即可;
(2)求出h(x)的解析式,根据h(1)≥2,得到关于m的不等式,通过讨论m的范围结合函数的单调性确定m的值即可.
解答 解:(1)${f^'}(x)=\frac{{-a{x^2}+x+a-1}}{x^2}$,又f(x)在x=2处取得极值,则${f^'}(2)=0⇒a=\frac{1}{3}$,
此时${f^'}(x)=\frac{(x-1)(x-2)}{{-3{x^2}}}$,显然满足条件,所以a的值为$\frac{1}{3}$.
(2)由条件$h(x)=ln(mx+\frac{1}{2})+\frac{2}{2x+1}+1$,又h(x)在(0,+∞)上的最小值为2,
所以有h(1)≥2,即$ln(m+\frac{1}{2})+\frac{5}{3}≥2⇒ln(m+\frac{1}{2})≥\frac{1}{3}>0=ln1$$⇒m>\frac{1}{2}$
又${h^'}(x)=\frac{2m}{2mx+1}-\frac{4}{{{{(2x+1)}^2}}}=\frac{{8m{x^2}+2m-4}}{{(2mx+1){{(2x+1)}^2}}}$,
当m≥2时,可知h(x)在(0,+∞)上递增,无最小值,不合题意,
故这样的m必须满足$\frac{1}{2}<m<2$,此时,函数h(x)的增区间为$(\sqrt{\frac{2-m}{4m}},+∞)$,减区间为$(0,\sqrt{\frac{2-m}{4m}})$,$h{(x)_{min}}=h(\sqrt{\frac{2-m}{4m}})=ln(m\sqrt{\frac{2-m}{4m}}+\frac{1}{2})+\frac{2}{{2\sqrt{\frac{2-m}{4m}}+1}}+1=2$,
整理得$ln(\frac{{\sqrt{2m-{m^2}}+1}}{2})-\frac{{\sqrt{2-m}-\sqrt{m}}}{{\sqrt{2-m}+\sqrt{m}}}=0$(*)
若$\frac{1}{2}<m<1$,则$\sqrt{2-m}-\sqrt{m}>0$,且$ln(\frac{{\sqrt{2m-{m^2}}+1}}{2})<ln1=0$,无解
若1≤m<2,则$\sqrt{2-m}-\sqrt{m}<0$,将(*)变形为$ln(\frac{{\sqrt{2m-{m^2}}+1}}{2})+\frac{{\sqrt{2-m}-\sqrt{m}}}{{\sqrt{2-m}+\sqrt{m}}}=0$.
即$ln(\frac{{\sqrt{2m-{m^2}}+1}}{2})+\frac{{\sqrt{2-m}-\sqrt{m}}}{{\sqrt{2-m}+\sqrt{m}}}=0$,设$t=\frac{{\sqrt{2m-{m^2}}+1}}{2}∈(\frac{1}{2},1]$
则上式即为$lnt+\sqrt{\frac{1}{t}-1}=0$,构造$F(t)=lnt+\sqrt{\frac{1}{t}-1}$,
则等价于F(t)=0${F^'}(t)=\frac{{2\sqrt{t-{t^2}}-1}}{{2t\sqrt{t-{t^2}}}}≤0$,故F(t)在$(\frac{1}{2},1]$上单调递减,
又F(1)=0,故F(t)=0等价于t=1,与之对应的m=1,
综上,m=1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | [-1,3] | B. | [1,3] | C. | [1,2] | D. | (-∞,3] |
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )| A. | $3-\frac{{\sqrt{2}}}{4}$ | B. | $3+\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | $3+\;\frac{{\sqrt{17}}}{2}$ |
| A. | tanx | B. | sinx | C. | cosx | D. | $\frac{1}{tanx}$ |
| A. | -sin2x | B. | sin2x | C. | -2sin2x | D. | 2sin2x |
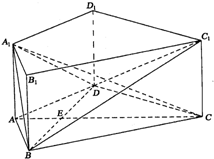 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,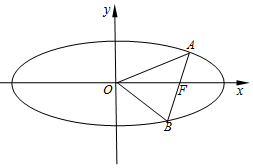 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.