题目内容
双曲线2x2-y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:双曲线2x2-y2=1中,a=
,b=1,求出c,即可求出双曲线2x2-y2=1的离心率.
| ||
| 2 |
解答:
解:双曲线2x2-y2=1中,a=
,b=1,
∴c=
=
,
∴双曲线2x2-y2=1的离心率e=
=
,
故选:C.
| ||
| 2 |
∴c=
|
| ||
| 2 |
∴双曲线2x2-y2=1的离心率e=
| c |
| a |
| 3 |
故选:C.
点评:本题考查双曲线的离心率,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知M=
(a,θ∈R,a≠0),则M的最大值与最小值分别为( )
| a2+asinθ+1 |
| a2+acosθ+1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
函数f(x)=4x-x4的图象大致是( )
A、 |
B、 |
C、 |
D、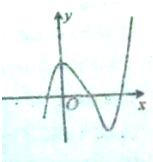 |
已知函数f(x)=
,若不等式f(x)<0的解集为非空集合D,且D⊆(-1,2),则z=2a-b的取值范围为( )
|
| A、(4,+∞) |
| B、[-4,+∞) |
| C、(-∞,4) |
| D、(-1,4) |
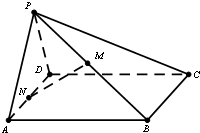 如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.
如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.