题目内容
设函数f（x）=
则x＞0时，f[f（x）]表达式中的展开式中的常数项为 ．（用数字作答）
|
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得x＞0时，f（x）=-
＜0，f[f（x）]=[
-2f(x)]6，它的通项公式为 Tr+1=
•（-2）r•[f（x）]2r-6，令x的幂指数等于零，求得r的值，可得f[f（x）]表达式中的展开式中的常数项．
| x |
| 1 |
| f(x) |
| C | r 6 |
解答：
解：∴函数f（x）=
，则x＞0时，f（x）=-
＜0，
∴f[f（x）]=[
-2f(x)]6，它的通项公式为 Tr+1=
•（-2）r•[f（x）]2r-6，
令2r-6=0，求得r=3，可得f[f（x）]表达式中的展开式中的常数项为
•（-2）3=-160，
故答案为：-160．
|
| x |
∴f[f（x）]=[
| 1 |
| f(x) |
| C | r 6 |
令2r-6=0，求得r=3，可得f[f（x）]表达式中的展开式中的常数项为
| C | 3 6 |
故答案为：-160．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，分段函数的应用，属于中档题．
练习册系列答案
相关题目
已知M=
（a，θ∈R，a≠0），则M的最大值与最小值分别为（ ）
| a2+asinθ+1 |
| a2+acosθ+1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
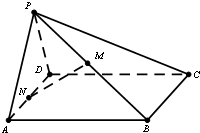如图，边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直，且M、N分别为PB、AD中点．