题目内容
已知直线l1：3x+4y-2=0和直线l2：2x+y+2=0，则l1与l2交点的坐标是 ；直线3x+4y-2+λ（2x+y+2）=0恒过定点 ．
考点：恒过定点的直线,两条直线的交点坐标
专题：直线与圆
分析：联立方程组即可求出直线的交点坐标，利用参数分离法即可求出直线过定点问题．
解答：
解：由
，解得
，即交点坐标为（-2，2），
若直线3x+4y-2+λ（2x+y+2）=0恒过定点，
则满足
，解得
，即定点坐标为（-2，2），
故答案为：（-2，2），（-2，2）．
|
|
若直线3x+4y-2+λ（2x+y+2）=0恒过定点，
则满足
|
|
故答案为：（-2，2），（-2，2）．
点评：本题主要考查直线的交点坐标的求解，解方程组是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
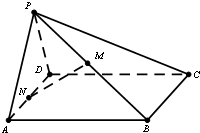如图，边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直，且M、N分别为PB、AD中点．