题目内容
11.已知函数$f(x)=sin(2x+\frac{7π}{4})+cos(2x-\frac{3π}{4})$,x∈R.(1)求f(x)的最小正周期和单调增区间;
(2)已知$cos(β-α)=\frac{4}{5}$,$cos(β+α)=-\frac{4}{5}$,$0<α<β≤\frac{π}{2}$,求f(β).
分析 (1)利用诱导公式化简函数解析式为f(x)=2sin(2x-$\frac{π}{4}$),利用三角函数周期公式可求最小正周期,利用$2kπ-\frac{π}{2}≤2x-\frac{π}{4}≤2kπ+\frac{π}{2}$,可求函数的单调增区间.
(2)利用两角和与差的余弦函数公式化简可得2cosβcosα=0,结合角的范围可求$β=\frac{π}{2}$,代入即可得解.
解答 解:(1)因为$f(x)=sin(2x+\frac{7π}{4}-2π)+sin(2x-\frac{3π}{4}+\frac{π}{2})$=$sin(2x-\frac{π}{4})+sin(2x-\frac{π}{4})=2sin(2x-\frac{π}{4})$,
所以T=π,
由$2kπ-\frac{π}{2}≤2x-\frac{π}{4}≤2kπ+\frac{π}{2}$,得单调增区间为$[{kπ-\frac{π}{8},kπ+\frac{3π}{8}}]$,k∈Z.
(2)∵$cos(β-α)=\frac{4}{5}$,$cos(β+α)=-\frac{4}{5}$,
∴$cosβcosα+sinβsinα=\frac{4}{5}$,$cosβcosα-sinβsinα=-\frac{4}{5}$,
两式相加,得2cosβcosα=0,
∵$0<α<β≤\frac{π}{2}$,
∴$β=\frac{π}{2}$,
由(1)知$f(β)=2sin(2β-\frac{π}{4})=\sqrt{2}$.
点评 本题主要考查了诱导公式,两角和与差的余弦函数公式在三角函数化简求值中的应用,考查了正弦函数的图象和性质及三角函数周期公式的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
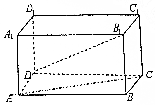 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.