题目内容
4.命题:“若m≤0,或n≤0,则m+n≤0”.(1)写出上面命题的逆命题,否命题,逆否命题,并判断它们的真假;
(2)说明原命题中条件与结论的充分性与必要性.
分析 (1)分别写出其逆命题,否命题,逆否命题并判断即可;(2)根据充分必要条件的定义判断即可.
解答 解:(1)原命题:“若m≤0,或n≤0,则m+n≤0”,这是假命题.
逆命题:若m+n≤0,则m≤0,或n≤0,这是真命题.…(4分)
否命题:若m>0,且n>0,则m+n>0,这是真命题.…(8分)
逆否命题:若m+n>0,则m>0,且n>0,这是假命题.…(12分)
(2)条件p:m≤0,或n≤0,结论q:m+n≤0.
由(1)知p推不出q,q⇒p,故p是q的必要不充分条件.…(17分)
由(1)知:p推不出q,q⇒p,
故p是q的必要不充分条件.
点评 本题考查了四种命题的关系,考查充分必要条件,是一道基础题.

练习册系列答案
相关题目
14.已知集合A={1,2,3},B={x|(x-3)(x-6)=0},则A∩B等于( )
| A. | {1} | B. | {2,3} | C. | {3,6} | D. | {3} |
19.已知A,B是球O的球面上两点,∠AOB=60°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{{16\sqrt{3}}}{3}$,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 144π | D. | 256π |
16.过直线3x-2y+3=0与x+y-4=0的交点,与直线2x+y-1=0平行的直线方程为( )
| A. | 2x+y-5=0 | B. | 2x-y+1=0 | C. | x+2y-7=0 | D. | x-2y+5=0 |
14.抛物线x=-4y2的准线方程为( )
| A. | y=1 | B. | y=$\frac{1}{16}$ | C. | x=1 | D. | x=$\frac{1}{16}$ |
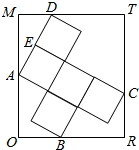 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.