题目内容
19．已知A，B是球O的球面上两点，∠AOB=60°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为$\frac{{16\sqrt{3}}}{3}$，则球O的表面积为（ ）| A． | 36π | B． | 64π | C． | 144π | D． | 256π |
分析 当点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大，利用三棱锥O-ABC体积的最大值为$\frac{{16\sqrt{3}}}{3}$，求出半径，即可求出球O的表面积．
解答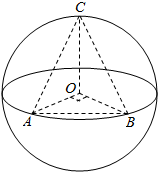 
解：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大，设球O的半径为R，此时VO-ABC=VC-AOB=$\frac{1}{3}×\frac{1}{2}{R}^{2}×\frac{\sqrt{3}}{2}$×R=$\frac{{16\sqrt{3}}}{3}$，
故R=4，则球O的表面积为4πR2=64π，
故选B．
点评 本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大是关键．
练习册系列答案
阅读快车系列答案
相关题目
10．“a=-5”是“直线y=x+4与圆（x-a）2+（y-3）2=8相切”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
7．线段x-2y+1=0（-1≤x≤3）的垂直平分线方程为（ ）
| A． | x+2y-3=0 | B． | 2x+y-3=0 | C． | 2x+y-1=0 | D． | 2x-y-1=0 |
8．（log29）•（log34）等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 4 |