题目内容
14．抛物线x=-4y2的准线方程为（ ）| A． | y=1 | B． | y=$\frac{1}{16}$ | C． | x=1 | D． | x=$\frac{1}{16}$ |
分析 将方程化为标准方程，再由y2=-2px的准线方程为x=$\frac{p}{2}$，即可得到所求．
解答 解：抛物线x=-4y2即为
y2=-$\frac{1}{4}$x，
可得准线方程为x=$\frac{1}{16}$．
故选：D．
点评 本题考查抛物线的方程和性质，主要考查准线方程的求法，注意化方程为标准方程，属于基础题．
练习册系列答案
相关题目
2．
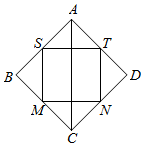如图，记正方形ABCD四条边的中点为S、M、N、T，连接四个中点得小正方形SMNT．将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1，V2，则V1：V2=（ ）
如图，记正方形ABCD四条边的中点为S、M、N、T，连接四个中点得小正方形SMNT．将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1，V2，则V1：V2=（ ）| A． | 8：1 | B． | 2：1 | C． | 4：3 | D． | 8：3 |
19．设函数$f（x）=\left\{\begin{array}{l}3x-1，\;x＜3\\{2^x}，\;x≥3\end{array}\right.$，则满足f（f（a））=2f（a）的a取值范围是（ ）
| A． | $[{\frac{2}{3}，\;\frac{4}{3}}]$ | B． | $[{\frac{2}{3}，\;+∞}）$ | C． | $[{\frac{4}{3}，\;+∞}）$ | D． | $[{\frac{4}{3}，\;+∞}]∪\left\{{\frac{2}{3}}\right\}$ |
6．“0＜a＜3”是“双曲线$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{9}$=1（a＞0）的离心率大于2”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
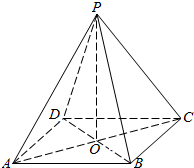如图，O为正四棱锥P-ABCD的底面中心，该棱锥的侧棱长和底面边长都是2．试求：