题目内容
1．设命题p：?n∈N，n2＞2n，则?p为（ ）| A． | ?n∈N，n2＞2n | B． | ?n∈N，n2＞2n | C． | ?n∈N，n2≤2n | D． | ?n∈N，n2≤2n |
分析 直接利用特称命题的否定是全称命题写出结果即可．
解答 解：因为特称命题的否定是全称命题，所以命题的否定为：?n∈N，n2≤2n
故选C．
点评 本题考查命题的否定特称命题与全称命题的关系，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
11．两条平行线l1，l2分别过点P（-1，2），Q（2，-3），它们分别绕P，Q旋转，但始终保持平行，则l1，l2之间距离的取值范围是（ ）
| A． | （5，+∞） | B． | （0，5] | C． | $（\sqrt{34}，+∞）$ | D． | $（0，\sqrt{34}]$ |
12．对两个变量进行回归分析，则下列说法中不正确的是（ ）
| A． | 有样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必经过样本中心（$\overline{x}$，$\overline{y}$） | |
| B． | 残差平方和越大，模型的拟合效果越好 | |
| C． | 用R2来刻画回归效果，R2越大，说明模型的拟合效果越好 | |
| D． | 若散点图中的样本呈条状分布，则变量y和x之间具有线性相关关系 |
9．已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π）满足f（-x）=f（x），其图象与直线y=2的某两个交点横坐标为分别为x1，x2，且|x1-x2|的最小值为π，则（ ）
| A． | $ω=\frac{1}{2}，φ=\frac{π}{4}$ | B． | $ω=2，φ=\frac{π}{4}$ | C． | $ω=\frac{1}{2}，φ=\frac{π}{2}$ | D． | $ω=2，φ=\frac{π}{2}$ |
16．ab≥0是|a-b|=|a|-|b|的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
6．某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示：
（1）设该企业每天生产甲、乙两种产品分别为x，y吨，试写出关于的线性约束条件并画出可行域；
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润．
| 甲 | 乙 | 原料限额 | |
| A（吨） | 3 | 2 | 12 |
| B（吨） | 1 | 2 | 8 |
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润．
13．已知集合A={-1，0，1，2}，B={x|x（x-2）＜0}，则A∩B等于（ ）
| A． | {0} | B． | {-1} | C． | {1} | D． | {0，-1，1} |
10．已知函数$f（x）={cos^2}x+sinx，x∈[\frac{π}{3}，\frac{5π}{6}]$，则f（x）的最大值与最小值的和为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{{2\sqrt{3}+5}}{4}$ | D． | $\frac{{2\sqrt{3}+6}}{4}$ |
11．某几何体的三视图如图所示，则该几何体的体积为（ ）
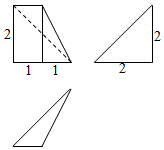
| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | $\frac{8}{3}$ |