题目内容
17.如图在空间四边形OABC中,点M在OA上,且OM=2MA,N为BC中点,则$\overrightarrow{MN}$等于( )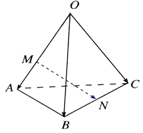
| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
分析 利用向量多边形与三角形法则即可得出.
解答 解:$\overrightarrow{MN}$=$\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}$=$\frac{1}{3}\overrightarrow{OA}$+$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{BC}$=$\frac{1}{3}\overrightarrow{OA}$+$(\overrightarrow{OB}-\overrightarrow{OA})$+$\frac{1}{2}(\overrightarrow{OC}-\overrightarrow{OB})$=$-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$.
故选:B.
点评 本题考查了向量多边形与三角形法则,考查了推理能力由于计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知随机变量ξ~B(5,$\frac{1}{3}$),则P(ξ=3)=( )
| A. | $\frac{5}{27}$ | B. | $\frac{7}{81}$ | C. | $\frac{40}{243}$ | D. | $\frac{19}{144}$ |
12.已知直线mx+4y-2=0与2x-5y+1=0互相垂直,则m的值为( )
| A. | 10 | B. | 20 | C. | 0 | D. | -4 |
2.下列说法不正确的是( )
| A. | “若xy=0,则x=0或y=0”的否命题是真命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是“?x∈R,x2-x-1≥0” | |
| C. | ?x∈R,使得ex<x-1 | |
| D. | “a<0”是“x2+ay2=1表示双曲线”的充要条件. |
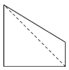
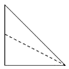
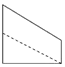
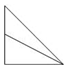
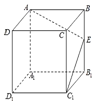 如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )