题目内容
9.在区间[1,6]和[2,4]上分别各取一个数,记为m和n,则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是$\frac{3}{5}$.分析 本题考查的知识点是几何概型的意义,关键是要找出方程 $\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆时(m,n)点对应的平面图形的面积大小和区间[1,6]和[2,4]分别各取一个数(m,n)点对应的平面图形的面积大小,并将他们一齐代入几何概型计算公式进行求解.
解答 解:若方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆,则m>n
在区间[1,6]和[2,4]上分别各取一个数,记为m和n,其面积为5×2=10,
满足m>n图形的面积为$\frac{(2+4)×2}{2}$=6
则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率P=$\frac{6}{10}$=$\frac{3}{5}$,
故答案为$\frac{3}{5}$.
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
17.如图在空间四边形OABC中,点M在OA上,且OM=2MA,N为BC中点,则$\overrightarrow{MN}$等于( )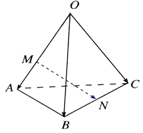

| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
18.若复数(m2-3m)+(m2-5m+6)i(m∈R))是纯虚数,则m的值为( )
| A. | 0 | B. | 2 | C. | 0或3 | D. | 2或3 |
19.已知α,β∈(0,$\frac{π}{2}$),cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,则角β=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{4}$ |