题目内容
2.下列说法不正确的是( )| A. | “若xy=0,则x=0或y=0”的否命题是真命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是“?x∈R,x2-x-1≥0” | |
| C. | ?x∈R,使得ex<x-1 | |
| D. | “a<0”是“x2+ay2=1表示双曲线”的充要条件. |
分析 A,原命题的否命题是:“如果xy≠0,则x≠0且y≠0”为真命题;
B,命题“?x∈R,x2-x-1<0”的否定是“?x∈R,x2-x-1≥0”;
C,设f(x)=ex-x+1,则f′(x)=ex-1,利用导数求出单调区间,求出函数f(x)的最小值即可;
D,a<0”时,“x2+ay2=1表示双曲线”;,“x2+ay2=1表示双曲线时,a<0;
解答 解:对于A,“若xy=0,则x=0或y=0”的否命题是:“如果xy≠0,则x≠0且y≠0”为真命题,正确;
对于B,命题“?x∈R,x2-x-1<0”的否定是“?x∈R,x2-x-1≥0”,正确;
对于C,设f(x)=ex-x+1,则f′(x)=ex-1,∴当x=0时,f′(x)=0.当x>0时,f′(x)>0,∴f(x)在(0,+∞)上是增函数,
当x<0时,f′(x)<0,∴f(x)在(-∞,0)上是减函数,∴f(x)>f(0)=1.∴对x∈R都有f(x)>0,∴ex>x-1,故错;
对于D,a<0”时,“x2+ay2=1表示双曲线”;,“x2+ay2=1表示双曲线时,a<0,故正确.
故选:C
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
相关题目
17.如图在空间四边形OABC中,点M在OA上,且OM=2MA,N为BC中点,则$\overrightarrow{MN}$等于( )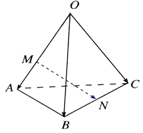

| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
11.已知椭圆$C:\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点为F点,P为椭圆C上一动点,定点A(2,4),则|PA|-|PF|的最小值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{17}$ | D. | $-\sqrt{17}$ |
12.数列3,5,9,17,33,…的通项公式an等于( )
| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 2n+1 |