已知随机变量ξ-B.则PA．$\frac{5}{27}$B．$\frac{7}{81}$C．$\frac{40}{243}$D．$\frac{19}{144}$ 题目和参考答案——青夏教育精英家教网—

题目内容

5．已知随机变量ξ～B（5，$\frac{1}{3}$），则P（ξ=3）=（　　）

A．

$\frac{5}{27}$

B．

$\frac{7}{81}$

C．

$\frac{40}{243}$

D．

$\frac{19}{144}$

分析随机变量ξ～B（5，$\frac{1}{3}$），可得P（ξ=3）=${C}_{5}^{3}•（\frac{1}{3}）^{3}（\frac{2}{3}）^{2}$，即可得出结论．

解答解：∵随机变量ξ～B（5，$\frac{1}{3}$），
∴P（ξ=3）=${C}_{5}^{3}•（\frac{1}{3}）^{3}（\frac{2}{3}）^{2}$=$\frac{40}{243}$，
故选C．

点评本题考查了二项分布与n次独立重复试验的模型，属于基础题．

练习册系列答案

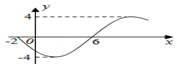
$y=-4sin（\frac{π}{8}x-\frac{π}{4}）$

B．

$y=4sin（\frac{π}{8}x-\frac{π}{4}）$

C．

$y=-4sin（\frac{π}{8}x+\frac{π}{4}）$

D．

$y=4sin（\frac{π}{8}x+\frac{π}{4}）$

16．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁，F₂，过F₁且与x轴垂直的直线交椭圆于A、B两点，直线AF₂与椭圆的另一个交点为C，若S_△ABC=3S${\;}_{△BC{F}_{2}}$，则椭圆的离心率为$\frac{\sqrt{5}}{5}$．

13．已知数列{a_n}满足a_n+2=a_n+1-a_n，且a₁=2，a₂=3，则a₂₀₁₇的值为2．

20．已知函数f（x）=x²-2x+alnx（a∈R）．
（Ⅰ）当a=2时，求函数f（x）在（1，f（1））处的切线方程；
（Ⅱ）当a＞0时，若函数f（x）有两个极值点x₁，x₂（x₁＜x₂），不等式f（x₁）≥mx₂恒成立，求实数m的取值范围．

10．已知抛物线C：y²=2px（p＞0）的焦点为F，P为C上异于原点的任意一点，过点P的直线l交C于另一点Q，交x轴的正半轴于点S，且有|FP|=|FS|．当点P的横坐标为3时，|PF|=|PS|．
（Ⅰ）求C的方程；
（Ⅱ）若直线l₁∥l，且l₁和C有且只有一个公共点E．
（ⅰ）证明直线PE过定点，并求出定点坐标；
（ⅱ）△PQE的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

17．如图在空间四边形OABC中，点M在OA上，且OM=2MA，N为BC中点，则$\overrightarrow{MN}$等于（　　）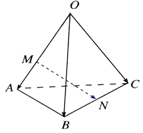

A．

$\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$

B．

$-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$

C．

$\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$

D．

$\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$

14．设命题p：“对任意的x∈R，x²-2x＞a”，命题q：“函数f（x）=x²+2ax+2-a在R上有零点”．如果命题p∨q为真，命题p∧q为假，求实数a的取值范围．

15．中心在坐标原点，离心率为 $\frac{5}{3}$且实轴长为6的双曲线的焦点在 x 轴上，则它的渐近线方程是（　　）

试题分类