题目内容
16.将函数y=-sin($\frac{π}{3}$-x)的周期变为原来的2倍,再将新函数图象向右平移$\frac{π}{6}$个单位长度,得到y=f(x)的图象,则函数y=f(x)的解析式为y=sin($\frac{1}{2}$x-$\frac{5π}{12}$).分析 由三角函数图象变换规律可得.
解答 解:变形可得函数y=-sin($\frac{π}{3}$-x)=sin(x-$\frac{π}{3}$),
周期变为原来的2倍得到y=sin($\frac{1}{2}$x-$\frac{π}{3}$)图象,
再将新函数图象向右平移$\frac{π}{6}$个单位长度得到y=sin[$\frac{1}{2}$(x-$\frac{π}{6}$)-$\frac{π}{3}$]图象,
变形可得y=sin($\frac{1}{2}$x-$\frac{5π}{12}$)
故答案为:y=sin($\frac{1}{2}$x-$\frac{5π}{12}$).
点评 本题考查三角函数图象变换,属基础题.

练习册系列答案
相关题目
7.已知点P(cosθ,sin2θ)和点Q(0,1)是两个相异点,则P、Q两点连线所在直线的倾斜角的取值范围为( )
| A. | [0,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
1.已知a3+a-3=a+a-1,则a2等于( )
| A. | 1 | B. | 3$+\sqrt{5}$ | C. | 2$+\sqrt{3}$ | D. | 3$+\sqrt{13}$ |
20.设等差数列{an}满足a2=7,a4=3,Sn是数列{an}的前n项和,则使得Sn>0最大的自然数n是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
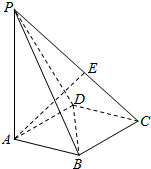 如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.
如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.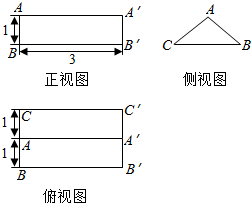 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).