题目内容
设x>0,求证:
<ln
<
.
| 1 |
| x+1 |
| x+1 |
| x |
| 1 |
| x |
考点:不等式的证明
专题:证明题,导数的综合应用,不等式的解法及应用
分析:令
=t,则x=
(t>1),原不等式即为1-
<lnt<t-1.令f(t)=t-1-lnt,g(t)=lnt-1+
,分别求出它们的导数,判断在t>1上的单调性,再由单调性即可得证.
| x+1 |
| x |
| 1 |
| t-1 |
| 1 |
| t |
| 1 |
| t |
解答:
证明:令
=t,则x=
(t>1),
原不等式即为1-
<lnt<t-1.
令f(t)=t-1-lnt,f′(t)=1-
,
当t>1时,f′(t)>0,即f(t)在t>1时递增,
即有f(t)>f(1)=0,
即为lnt<t-1;
令g(t)=lnt-1+
,g′(t)=
-
=
,
当t>1时,g′(t)>0,即g(t)在t>1递增,
则g(t)>g(1)=0,
即为lnt>1-
.
即有1-
<lnt<t-1.
故有原不等式成立.
| x+1 |
| x |
| 1 |
| t-1 |
原不等式即为1-
| 1 |
| t |
令f(t)=t-1-lnt,f′(t)=1-
| 1 |
| t |
当t>1时,f′(t)>0,即f(t)在t>1时递增,
即有f(t)>f(1)=0,
即为lnt<t-1;
令g(t)=lnt-1+
| 1 |
| t |
| 1 |
| t |
| 1 |
| t2 |
| t-1 |
| t2 |
当t>1时,g′(t)>0,即g(t)在t>1递增,
则g(t)>g(1)=0,
即为lnt>1-
| 1 |
| t |
即有1-
| 1 |
| t |
故有原不等式成立.
点评:本题考查不等式的证明,考查换元法和运用导数证明不等式,考查推理能力,属于中档题.

练习册系列答案
相关题目
不等式1≤|x-2|≤7的解集为( )
| A、{x|x≤1或x≥3} |
| B、{x|1≤x≤3} |
| C、{x|-5≤x≤1或3≤x≤9} |
| D、{x|-5≤x≤9} |
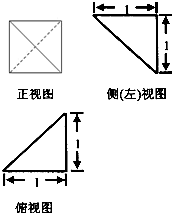
一个四面体的三视图如图所示,则该四面体的四个面中最大的面积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
方程(x-y-3)(x+y)=0所表示的图形是( )
| A、两条互相平行的直线 | ||||
| B、两条互相垂直的直线 | ||||
C、一个点(
| ||||
D、过点(
|
已知x+x-1=3,那么与x2-x-2的值为( )
A、3
| ||
B、-
| ||
C、±3
| ||
D、±
|