Question

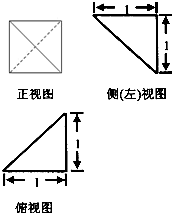
一个四面体的三视图如图所示，则该四面体的四个面中最大的面积是（　　）

• A、

  3

  2

• B、

  2

  2

• C、

  3

  4

• D、

  1

  2

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：将该几何体放入边长为1的正方体中，画出图形，根据图形，结合三视图，求出答案即可．

解答： 解：将该几何体放入边长为1的正方体中，如图所示，
由三视图可知该四面体为A-BA₁C₁，
由直观图可知，最大的面为BA₁C₁；
在等边三角形BA₁C₁ 中A₁B=

2

，
所以面积S=

1

2

×(

2

)2×sin

π

3

=

3

2

．
故选：A．

点评：本题考查了空间几何体的三视图的应用问题，解题的关键是由三视图得出几何体的结构特征是什么．