题目内容

不等式1≤|x-2|≤7的解集为（　　）
A、{x|x≤1或x≥3}
B、{x|1≤x≤3}
C、{x|-5≤x≤1或3≤x≤9}
D、{x|-5≤x≤9}
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由题意可得可得1≤x-2≤7，或-7≤x-2≤-1，由此求得x的范围．
解答： 解：由1≤|x-2|≤7，可得 1≤x-2≤7，或-7≤x-2≤-1，
求得3≤x≤9，或-5≤x≤1，
故选：C．
点评：本题主要考查绝对值不等式的解法，体现了等价转化和分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
点P（x，y）在不等式组
x-2≤0
y-1≤0
x+2y-2≥0
表示的平面区域上运动，则z=x+y的最大值为
 
．
直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线C1：
x=3+cosθ
y=4+sinθ
（θ为参数）和曲线C2：ρ=1上，则|AB|的最小值为
 
．
下列各式正确的是（　　）
A、0•
a
=
0
B、0•
a
=0
C、0•a=
0
D、
0
•a=0
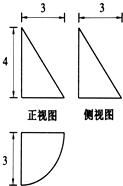某几何体的三视图（单位：cm）如图所示，其中俯视图中的曲线是四分之一的圆弧，则该几何体的体积等于
 
cm3，表面积等于
 
cm2．
已知△ABC的三个顶点的坐标分别是A（5，1），B（7，-3），C（2，-8），求它的外接圆的半径及方程．
函数y=cos2x+sinx的值域为
 
．
设x＞0，求证：
1
x+1
＜ln
x+1
x
＜
1
x
．
已知集合M={x|2x＞1}，若a∉M，则实数a可以是（　　）
A、3B、2C、1D、-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网