题目内容
16．已知双曲线C的一个焦点与抛物线${C_1}：{y^2}=-16x$的焦点重合，且其离心率为2．（1）求双曲线C的方程；
（2）求双曲线C的渐近线与抛物线C1的准线所围成三角形的面积．
分析 （1）$c=4，\frac{c}{4}=2$，可得a2=4，b2=12，即可求双曲线C的方程；
（2）双曲线C的渐近线方程y=±$\sqrt{3}$x与抛物线C1的准线x=4，联立得交点坐标求双曲线C的渐近线与抛物线C1的准线所围成三角形的面积．
解答 解：（1）$c=4，\frac{c}{4}=2$．∴a2=4，b2=12，双曲线C的方程$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1，
（2）双曲线C的渐近线方程y=±$\sqrt{3}$x与抛物线C1的准线x=4，联立得交点坐标为$（4，4\sqrt{3}），（4，-4\sqrt{3}）$，
所以三角形的面积为$S=16\sqrt{3}$．
点评 本题考查双曲线的方程与性质，考查抛物线的性质，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的焦距为$2\sqrt{5}$，且双曲线的一条渐近线方程为x-2y=0，则双曲线的方程为（ ）
| A． | $\frac{x^2}{4}-{y^2}=1$ | B． | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | C． | $\frac{{3{x^2}}}{20}-\frac{{3{y^2}}}{5}=1$ | D． | $\frac{{3{x^2}}}{5}-\frac{{3{y^2}}}{20}=1$ |
11．
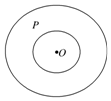如图，“天宫一号”运行的轨迹是如图的两个类同心圆，小圆的半径为2km，大圆的半径为4km，卫星P在圆环内无规则地自由运动，运行过程中，则点P与点O的距离小于3km的概率为（ ）
如图，“天宫一号”运行的轨迹是如图的两个类同心圆，小圆的半径为2km，大圆的半径为4km，卫星P在圆环内无规则地自由运动，运行过程中，则点P与点O的距离小于3km的概率为（ ）| A． | $\frac{1}{12}$ | B． | $\frac{5}{12}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{5}$ |
如图，在四棱锥P-ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD．
5．已知△ABC的边长为a，b，c，定义它的等腰判别式为D=max{a-b，b-c，c-a}+min{a-b，b-c，c-a}，则“D=0”是△ABC为等腰三角形的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |