题目内容
1.函数$f(x)=({x-\frac{1}{2}})({x-\frac{5}{2}})({x-\frac{7}{2}})$,数列{an}的通项公式an=|f(n)|,若数列从第k项起每一项随着n项数的增大而增大,则k的最小值为3.分析 x≥4时,利用导数研究函数的单调性即可得出.
解答 解:f(1)=$\frac{15}{8}$,f(2)=$\frac{9}{2}$,f(3)=-$\frac{5}{8}$,x≥4时,f(x)>0,f(4)=$\frac{21}{8}$,
x≥4时,f′(x)=$(x-\frac{5}{2})$$(x-\frac{7}{2})$+$(x-\frac{1}{2})$$(x-\frac{5}{2})$+$(x-\frac{7}{2})$$(x-\frac{1}{2})$>0,因此函数f(x)单调递增,f(x)≥f(4)>0.
a4>a3,
因此an单调递增.
∴数列从第3项起每一项随着n项数的增大而增大,则k的最小值为3.
故答案为:3.
点评 本题考查了利用导数研究函数的单调性、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.在空间直角坐标系中,点P(3,2,5)关于yOz平面对称的点的坐标为( )
| A. | (-3,2,5) | B. | (-3,-2,5) | C. | (3,-2,-5) | D. | (-3,2,-5) |
12.手表时针走过1小时,时针转过的角度( )
| A. | 60° | B. | -60° | C. | 30° | D. | -30° |
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为2,那么双曲线的渐近线方程为( )
| A. | $\sqrt{2}x±y=0$ | B. | x±y=0 | C. | 2x±y=0 | D. | $\sqrt{3}x±y=0$ |
16.已知随机变量服从正态分布N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.6 |
11.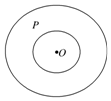 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |