题目内容
14.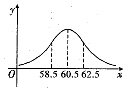 在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )
在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )附:若随机变量X服从正态分布N(u,σ2),
则P(u-σ<X<u+σ)=0.683,P(u-2σ<X<u+2σ)=0.954.
| A. | 954 | B. | 819 | C. | 683 | D. | 317 |
分析 由题意,P(58.5<X<62.5)=0.683,即可得出在这1000名男生中不属于正常情况的人数.
解答 解:由题意,P(58.5<X<62.5)=0.683,
∴在这1000名男生中不属于正常情况的人数是1000×(1-0.683)=317,
故选D.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,主要考查正态曲线的对称性,是一个基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.若集合A={x|x2-x-6>0},集合B={x|-1<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (2,4) | D. | (3,4) |
19.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| p(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
3.已知直线a,b,平面α,β,a?α,b?α,则a∥β,b∥β是α∥β的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
4.“m>1“是“函数f(x)=3x+m-3$\sqrt{3}$在区间[1,+∞)无零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
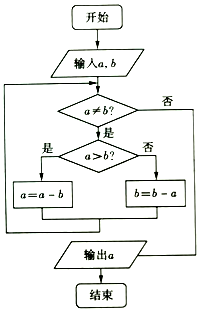 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )
如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )