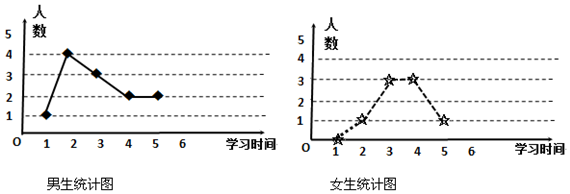
题目内容
4.“m>1“是“函数f(x)=3x+m-3$\sqrt{3}$在区间[1,+∞)无零点”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由“函数f(x)=3x+m-3$\sqrt{3}$在区间[1,+∞)无零点,得到m>$\frac{1}{2}$,再根据充分条件和必要的条件的定义即可判断.
解答 解:函数f(x)=3x+m-3$\sqrt{3}$在区间[1,+∞)无零点,
则3x+m>3$\sqrt{3}$,
即m+1>$\frac{3}{2}$,
解得m>$\frac{1}{2}$,
故“m>1“是“函数f(x)=3x+m-3$\sqrt{3}$在区间[1,+∞)无零点的充分不必要条件,
故选:A
点评 主要考查充分条件、必要条件、充要条件的定义,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.已知函数$f(x)={e^{{x^2}+2x}}$,设$a=lg\frac{1}{5}\;\;,\;\;b={log_{\frac{1}{2}}}\frac{1}{3}\;\;,\;\;c={({\frac{1}{3}})^{0.5}}$,则有( )
| A. | f(a)<f(b)<f(c) | B. | f(a)<f(c)<f(b) | C. | f(b)<f(c)<f(a) | D. | f(b)<f(a)<f(c) |
4.已知sinα=-$\frac{2}{3}$,则cos(π-2α)=( )
| A. | -$\frac{\sqrt{5}}{3}$ | B. | -$\frac{1}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{\sqrt{5}}{3}$ |
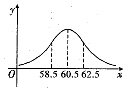 在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )
在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )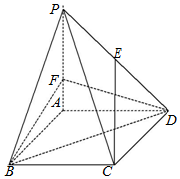 如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.