题目内容
设a=
(sinx+cosx)dx,则二项式(a
-
)6的展开式的常数项是 .
| ∫ | π 0 |
| x |
| 1 | ||
|
考点:二项式系数的性质
专题:函数的性质及应用
分析:求定积分可得a的值,在二项式的展开式中,令x的幂指数等于零,求得r的值,可得展开式的常数项.
解答:
解:∵a=
(sinx+cosx)dx=
=2,
则二项式(a
-
)6=(2
-
)6,
它的展开式的通项公式为Tr+1=(-1)r•
•26-r•x3-r,
令3-r=0,求得 r=3,故展开式的常数项是-
•26-3=-160,
故答案为:-160.
| ∫ | π 0 |
| (-cosx+sinx)| | π 0 |
则二项式(a
| x |
| 1 | ||
|
| x |
| 1 | ||
|
它的展开式的通项公式为Tr+1=(-1)r•
| C | r 6 |
令3-r=0,求得 r=3,故展开式的常数项是-
| C | 3 6 |
故答案为:-160.
点评:本题主要考查二项式定理的应用,求定积分,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
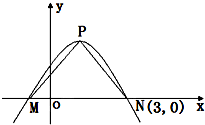 点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若
点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若