Question

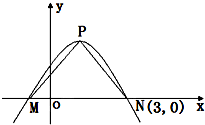点P是函数y=2sin（ωx+φ）（ω＞0）的图象的最高点，M，N是与点P相邻的且该图象与x轴的两个交点，且N（3，0），若

PM

•

PN

=0，则φ的值为（　　）

• A、

  π

  8

• B、

  π

  4

• C、4
• D、8

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由题意可得△PMN为等腰直角三角形，求得M（-1，0），P（1，2），由周期求的ω=

1

4

．再由五点法作图求得φ的值．

解答： 解：由题意可得△PMN为等腰直角三角形，斜边上的高等于2，故斜边长等于4，
再根据N（3，0），可得M（-1，0），
∴P（1，2），

1

2

•

2π

ω

=4，解得ω=

π

4

．
再由五点法作图可得

π

4

×（-1）+φ=0，
∴φ=

π

4

，
故选：B．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由周期求出ω，由五点法作图求出φ的值，